Đây là phần tiếp theo trong loạt bài “Khoa học máy tính thực tế”, nơi bạn sẽ học cách áp dụng các khái niệm khoa học máy tính cổ điển để giải quyết các vấn đề thực tế bằng cách sử dụng Ruby.
Hôm nay chúng ta sẽ nói về Lý thuyết đồ thị .
Bạn có thể đã nghe nói về cây nhị phân, chúng trông như thế này:
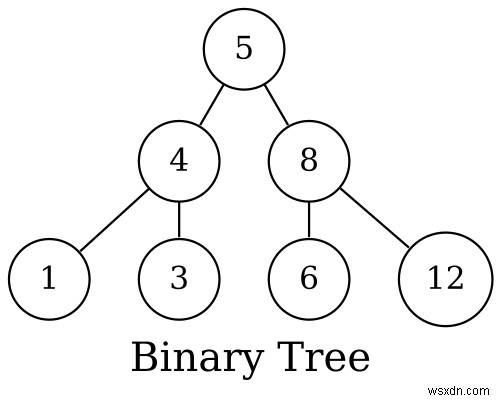
Vấn đề là cây nhị phân chỉ là một phiên bản chuyên biệt của đồ thị, do đó, điều đó sẽ cung cấp cho bạn ý tưởng về mức độ phổ biến của đồ thị.
Hãy bắt đầu với tổng quan về các nguyên tắc cơ bản của lý thuyết đồ thị, sau đó chúng ta sẽ xem một số ứng dụng thực tế và cách triển khai điều này trong Ruby là gì!
Các nguyên tắc cơ bản về biểu đồ
Một biểu đồ bao gồm hai yếu tố:
- Các nút (hoặc các đỉnh)
- Các cạnh
Một nút đại diện cho một phần tử trong biểu đồ, như thành phố hoặc đường phố, trong biểu đồ đại diện cho bản đồ. Trong khi các cạnh đại diện cho các kết nối giữa các nút.
Nếu bạn xem một cuốn sách khoa học máy tính hoặc toán học, bạn sẽ thấy một biểu đồ được xác định bởi công thức này:G(V, E) .
Ở đâu G nghĩa là Đồ thị, V là tập hợp các đỉnh &E là tập hợp các cạnh.
Đồ thị có thể được định hướng hoặc vô hướng. Có nghĩa là bạn chỉ có thể đi một hướng (đồ thị có hướng) hoặc cả hai hướng (đồ thị vô hướng).
Loại biểu đồ phổ biến nhất là Biểu đồ vòng tròn được hướng dẫn (DAG). Acyclic có nghĩa là không có vòng lặp, không có cách nào để quay lại.
Sử dụng cho đồ thị
Bây giờ chúng ta đã thấy tổng quan về các nguyên tắc cơ bản, hãy xem một số cách sử dụng phổ biến cho biểu đồ.
Sử dụng đồ thị, bạn có thể làm những việc như:
- Tìm đường đi ngắn nhất (hoặc dài nhất) giữa hai địa điểm
- Kiểm tra xem hai thứ có liên quan đến nhau không
- Xây dựng công cụ đề xuất
- Phân tích sự phụ thuộc
Một ví dụ khác bao gồm việc tìm kiếm tuyến đường tốt nhất đến điểm đến (hãy nghĩ đến thiết bị GPS).
Cách triển khai và sử dụng đồ thị
Bạn có thể viết cách triển khai đồ thị của riêng mình, nhưng đối với bài viết này, chúng tôi sẽ bám sát vào đá quý RGL đã triển khai một viên ngọc cho chúng tôi.
Để tạo một biểu đồ cơ bản bằng RGL:
require 'rgl/adjacency' graph = RGL::DirectedAdjacencyGraph.new graph.add_edge 1,2 graph.add_edge 3,4 graph.add_edge 1,4 graph.add_edge 4,3
Mã này tạo ra đồ thị sau:
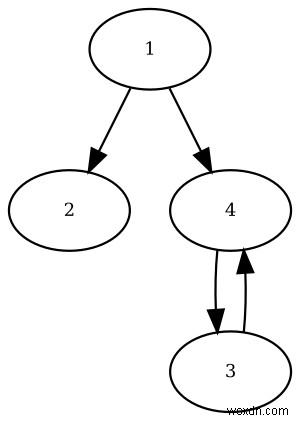
Bạn có thể nhận được một biểu diễn đồ họa của biểu đồ của bạn như sau:
require 'rgl/dot' graph.print_dotted_on
Sau đó, sao chép đầu ra của phương pháp đó trên một trang web có thể xử lý ngôn ngữ dấu chấm. Thích cái này.
Ngoài ra, bạn có thể cài đặt Graphviz trên máy của mình để tạo hình ảnh cục bộ.
Bây giờ chúng ta có một biểu đồ, chúng ta có thể muốn xem qua nó để tìm hiểu thông tin về nó.
Có hai thuật toán cơ bản để tìm kiếm biểu đồ của bạn :
- Tìm kiếm theo chiều rộng-Đầu tiên (BFS)
- Tìm kiếm theo chiều sâu-Đầu tiên (DFS)
Trong BFS, bạn có được các nút gần nhất trước tiên và trong DFS, bạn đi sâu nhất có thể cho mọi nút. Các thuật toán này có thể được triển khai bằng cách sử dụng cấu trúc dữ liệu ngăn xếp.
Đá quý RGL đã triển khai các thuật toán đó cho bạn:
require 'rgl/traversal' graph.bfs_iterator.to_a # [1, 2, 4, 3] graph.dfs_iterator.to_a # [1, 4, 3, 2]
Nhìn lại biểu đồ và đi theo con đường mà các thuật toán này đã thực hiện chỉ bằng mắt của bạn (hoặc bạn cũng có thể sử dụng ngón tay nếu muốn). Điều đó sẽ giúp bạn hiểu được những gì đang diễn ra.
Đồ thị có trọng số
Chúng tôi có thể thêm nhiều thông tin vào biểu đồ dưới dạng trọng số để làm cho nó hữu ích hơn.
Trọng số được trao cho các cạnh, là đường dẫn giữa hai nút (còn được gọi là "đỉnh"). Các trọng số này thể hiện chi phí đi từ điểm này đến điểm khác.
Ví dụ:nếu chúng ta có bản đồ của một quốc gia ở dạng biểu đồ và chúng ta muốn đến một điểm đến nhất định trong thời gian ngắn nhất có thể, trọng số sẽ đại diện cho khoảng cách giữa hai thành phố.
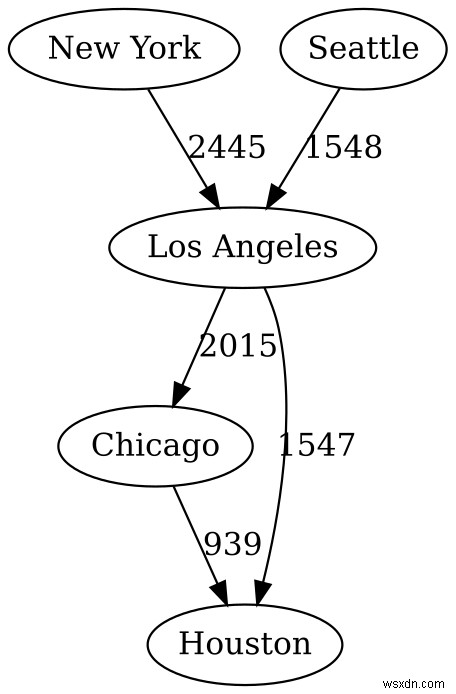
Hoặc nếu chúng ta có một mạng máy tính, trọng số có thể biểu thị số bước cần thiết để truy cập một mạng nhất định.
“Trong mạng máy tính, bước nhảy là một phần của đường dẫn giữa nguồn và đích. Các gói dữ liệu đi qua các cầu nối, bộ định tuyến và cổng khi chúng di chuyển giữa nguồn và đích. Mỗi khi các gói được chuyển đến thiết bị mạng tiếp theo, một bước nhảy sẽ xảy ra ”. - Wikipedia
Dưới đây là ví dụ về mã cho biểu đồ có trọng số:
graph = RGL::DirectedAdjacencyGraph.new
graph.add_vertices "Los Angeles", "New York", "Chicago", "Houston", "Seattle"
edge_weights =
{
["New York", "Los Angeles"] => 2445,
["Los Angeles", "Chicago"] => 2015,
["Los Angeles", "Houston"] => 1547,
["Chicago", "Houston"] => 939,
["Seattle", "Los Angeles"] => 1548
}
edge_weights.each { |(city1, city2), w| graph.add_edge(city1, city2) }
Bây giờ chúng ta có thể tìm kiếm đường đi ngắn nhất từ điểm này đến điểm khác. Và đó chính xác là chủ đề của phần tiếp theo!
Tìm con đường ngắn nhất
Một thuật toán phổ biến để tìm đường đi ngắn nhất bên trong biểu đồ là thuật toán “Đường đi ngắn nhất của Dijkstra”.
Với một biểu đồ có trọng số, chúng ta có thể sử dụng thuật toán Dijkstra để giải quyết câu hỏi này:
“Cách nhanh nhất để đi từ điểm A đến điểm B là gì?”
Đây là một ví dụ về mã, sử dụng đá quý RGL:
p graph.dijkstra_shortest_path(edge_weights, "New York", "Houston") # ["New York", "Los Angeles", "Houston"]
Điều này cho chúng ta biết con đường ngắn nhất từ New York đến Houston, sử dụng thông tin có sẵn trong biểu đồ.
Tóm tắt
Bạn đã biết cấu trúc dữ liệu biểu đồ là gì và cách sử dụng nó với đá quý RGL.
Bạn cũng đã tìm hiểu về các thuật toán phổ biến để làm việc với đồ thị, như DFS, BFS &Dijkstra’s.
Đừng quên chia sẻ bài đăng này nếu bạn thấy nó hữu ích để nhiều người có thể thưởng thức nó 🙂
