heap min-max đối xứng (SMMH) được định nghĩa là một cây nhị phân hoàn chỉnh trong đó mỗi nút ngoại trừ gốc có đúng một phần tử. Gốc của một SMMH là rỗng và tổng số nút trong SMMH là m + 1, trong đó m là số phần tử.
Gọi y là bất kỳ nút nào của SMMH. Gọi các phần tử (y) là các phần tử trong cây con bắt nguồn từ y nhưng loại trừ phần tử (nếu có) ở y. Giả sử rằng các phần tử (y) j =∅. bạn thỏa mãn các thuộc tính sau:
- Con bên trái của y có phần tử nhỏ nhất trong các phần tử (y).
- Con bên phải của y (nếu có) có phần tử tối đa trong các phần tử (y).
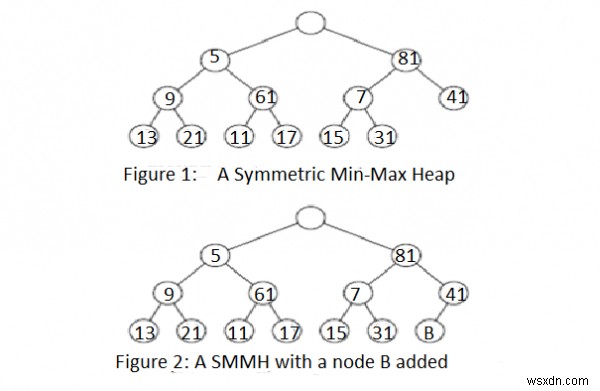
Hình 1 cho thấy một SMMH mẫu có 12 phần tử.
Khi y biểu thị nút có 81, các phần tử (y) ={7, 15, 31, 41}; con trái của y có phần tử nhỏ nhất là 6 trong các phần tử (y); và con bên phải của y có phần tử lớn nhất là 41 trong các phần tử (y). Chúng tôi có thể xác minh rằng mọi nút y của SMMH này đều đáp ứng các thuộc tính đã nêu.
Vì một SMMH được biểu thị là một cây nhị phân hoàn chỉnh, nó được lưu trữ dưới dạng một cấu trúc dữ liệu ngầm thực hiện ánh xạ tiêu chuẩn của một cây nhị phân hoàn chỉnh thành một mảng. Khi m =1, phần tử tối thiểu và tối đa giống nhau và được chứa trong phần tử con bên trái của phần tử gốc của SMMH.
Khi m> 1, phần tử nhỏ nhất nằm trong con trái của căn và cực đại nằm trong con bên phải của căn. Vì vậy, các hoạt động getMin và getMax tiêu tốn O (1) thời gian.
Dễ dàng thấy rằng cây nhị phân hoàn chỉnh m + 1 nút với gốc trống và một phần tử trong mọi nút khác là SMMH iff, điều sau là đúng -
A1 - Đối với mọi nút y có phần tử bên phải, phần tử trong y nhỏ hơn hoặc bằng phần tử trong phần tử bên phải của y.
A2 - Đối với mọi nút y có một nút ông, phần tử trong nút con bên trái của nút ông bà nhỏ hơn hoặc bằng phần tử trong y.
A3 - Đối với mọi nút y có một nút ông bà, phần tử trong nút con bên phải của nút ông bà lớn hơn hoặc bằng phần tử trong y.
Chú ý rằng nếu thuộc tính A1 được thỏa mãn tại nút y, thì nhiều nhất một trong A2 và A3 có thể bị vi phạm tại y. Thực hiện các thuộc tính từ A1 đến A3, chúng ta đạt được các Thuật toán đơn giản để chèn và loại bỏ các phần tử. Các Thuật toán này là sự thích nghi đơn giản của các Thuật toán tương ứng cho các đống tối thiểu và tối đa. Độ phức tạp của chúng là O (log m).
Ở đây, chúng tôi chỉ định thao tác chèn. Giả sử chúng ta muốn chèn 3 vào SMMH của Hình 1. Vì một SMMH là một cây nhị phân hoàn chỉnh, chúng ta phải thêm một nút mới vào SMMH ở vị trí như trong Hình 2; nút mới được gắn nhãn là B.
Trong ví dụ của chúng tôi, B sẽ biểu thị một nút trống. Bây giờ 3 được chèn vào nút B.
