Binomial Heap được định nghĩa là phần mở rộng của Binary Heap cung cấp phép hợp nhất hoặc tách đơn lẻ nhanh hơn cùng với các hoạt động khác được cung cấp bởi Binary Heap.
Một đống nhị thức được coi như một tập hợp các cây nhị thức.
Cây nhị thức là gì?
Cây nhị thức bậc k có thể được xây dựng bằng cách lấy hai cây nhị thức bậc k-1 và giảm bớt một cây là con ngoài cùng bên trái hoặc cây khác.
Cây Nhị thức bậc k có các thuộc tính dưới đây.
-
Số nút của Cây nhị thức có đúng 2 k .
-
Độ sâu của Cây nhị thức là k.
-
Có chính xác kCi nút ở độ sâu i trong đó i =0, 1,. . . , k.
-
Gốc có bậc k và con của gốc được coi là Cây nhị thức với thứ tự k-1, k-2, .. 0 từ trái sang phải.
Nhóm nhị thức -
Một đống nhị thức được định nghĩa là một tập hợp các cây nhị thức trong đó mỗi cây nhị thức tuân theo thuộc tính MinHeap. Và ở bất kỳ mức độ nào, có thể có tối đa một Cây nhị thức ở bất kỳ mức độ nào.
Ví dụ về đống nhị thức -
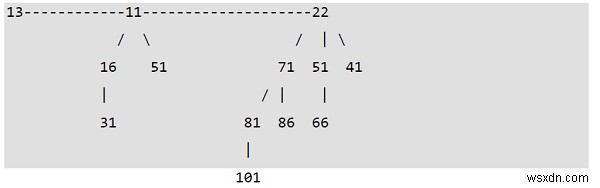
Một đống nhị thức có 12 nút. Nó được coi như một tập hợp của 2
Từ trái sang phải Cây nhị thức bậc 2 và 3

Các đống nhị thức và biểu diễn nhị phân của một số
Một đống nhị thức có m nút có số cây nhị thức bằng số bit tập hợp trong biểu diễn nhị phân của m. Ví dụ, giả sử m là 13, có 3 bit đặt trong biểu diễn nhị phân của m (00001101), cho biết 3 Cây nhị thức. Chúng ta cũng có thể liên hệ mức độ của các Cây nhị thức này với vị trí của các bit đã đặt. Với sự trợ giúp của mối quan hệ này, chúng ta có thể quyết định hoặc kết luận rằng có các Cây nhị thức O (logm) trong một Hầm Nhị thức với các nút ‘m’
Hoạt động của đống nhị thức -
union () là phép toán chính trong Binomial Heap, tất cả các phép toán khác chủ yếu thực hiện phép toán này. Phép toán union () chịu trách nhiệm kết hợp hai Nhóm nhị thức thành một.
-
insert (h, K) - Chèn khóa ‘K’ vào đống nhị thức ‘h’. Lúc đầu, thao tác này có thể tạo một đống nhị thức với một khóa duy nhất là ‘K’, sau đó gọi liên hợp trên h và đống nhị thức mới.
-
getMin (h) - Một phương pháp đơn giản để getMin () là truy cập danh sách gốc của Cây nhị thức và trả về khóa nhỏ nhất.
Ứng dụng này yêu cầu thời gian O (logm). Nó có thể được cải thiện thành O (1) bằng cách duy trì một gốc khóa nhỏ nhất của pointerto.
-
extractMin (h) - Thao tác này cũng thực hiện union (). Lúc đầu, chúng ta gọi getMin () để tính Cây nhị thức khóa nhỏ nhất, tiếp theo, chúng ta loại bỏ nút và tạo một Heap đơn thức mới bằng cách kết hợp tất cả các cây con của nút nhỏ nhất đã bị loại bỏ. Cuối cùng, chúng ta gọiunion () trên h cũng như Heap nhị thức mới được tạo. Thao tác này yêu cầu thời gian O (logm).
-
delete (h) - Tương tự như Binary Heap, lúc đầu, thao tác xóa sẽ giảm khóa thành trừ vô hạn, các cuộc gọi tiếp theo là extractMin ().
-
ReduceKey (h) - ReduceKey () cũng giống như Binary Heap. Lúc đầu, chúng tôi so sánh khóa của cơ sở hạ tầng với khóa gốc và nếu khóa của phụ huynh nhiều hơn, thì chúng tôi trao đổi khóa và lặp lại cho khóa chính. Cuối cùng, chúng tôi dừng lại khi chúng tôi đến một nút mà cha mẹ có một khóa nhỏ hơn hoặc chúng tôi đến nút gốc. Độ phức tạp thời gian của ReduceKey () là O (logm).
