Các kết nối quan trọng trong mạng bằng C ++

Giả sử có n máy chủ. Và chúng được đánh số từ 0 đến n-1 được kết nối bởi các kết nối máy chủ đến máy chủ được định hướng tạo thành một mạng mà các kết nối [i] =[a, b] đại diện cho kết nối giữa các máy chủ a và b. Tất cả các máy chủ được kết nối trực tiếp hoặc thông qua một số máy chủ khác. Bây giờ, một kết nối quan trọng là một kết nối, nếu bị loại bỏ, nó sẽ làm cho một số máy chủ không thể kết nối với một số máy chủ khác. Chúng tôi phải tìm tất cả các kết nối quan trọng.

Vì vậy, nếu đầu vào là n =4 và kết nối =[[0,1], [1,2], [2,0], [1,3]],

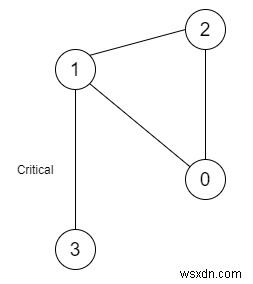
thì đầu ra sẽ là [[1,3]]

Để giải quyết vấn đề này, chúng tôi sẽ làm theo các bước sau -

• Xác định một tập hợp

• Xác định một đĩa mảng

• Xác định mức thấp của mảng

• Xác định một mảng 2D ret

• Xác định một hàm dfs (), điều này sẽ lấy nút, mệnh, một đồ thị mảng 2D,

• nếu nút nằm trong số được truy cập, thì -

  • trở lại

• chèn nút vào đã truy cập

• đĩa [nút]:=time

• thấp [node]:=time

• (tăng thời gian lên 1)

• cho tất cả các phần tử x trong biểu đồ [node]

  • nếu x giống mệnh, thì -

    • Bỏ qua phần sau, chuyển sang phần tiếp theo

  • nếu x không được truy cập, thì -

    • dfs (x, nút, đồ thị)

    • thấp [nút]:=tối thiểu của [nút] thấp và thấp [x]

    • nếu đĩa [node]

      • chèn {node, x} vào cuối ret

  • Nếu không

    • low [node]:=tối thiểu của [node] thấp và đĩa [x]

• Từ phương thức chính, thực hiện như sau -

  • đặt kích thước của đĩa là n + 1

  • đặt kích thước thấp nhất là n + 1

  • thời gian:=0

  • Xác định một mảng danh sách đồ thị kích thước n + 1

  • để khởi tạo i:=0, khi i

    • u:=v [i, 0]

    • w:=v [i, 1]

    • chèn w vào cuối biểu đồ [u]

    • chèn u vào cuối biểu đồ [w]

  • dfs (0, -1, đồ thị)

  • trả lại ret

Hãy cùng chúng tôi xem cách triển khai sau để hiểu rõ hơn -

Ví dụ

#include <bits/stdc++.h>
using namespace std;
void print_vector(vector<vector<auto> > v){
   cout << "[";
   for(int i = 0; i<v.size(); i++){
      cout << "[";
      for(int j = 0; j <v[i].size(); j++){
         cout << v[i][j] << ", ";
      }
      cout << "],";
   }
   cout << "]"<<endl;
}
class Solution {
   public:
   set<int> visited;
   vector<int> disc;
   vector<int> low;
   int time;
   vector<vector<int> > ret;
   void dfs(int node, int par, vector<int> graph[]) {
      if (visited.count(node))
      return;
      visited.insert(node);
      disc[node] = low[node] = time;
      time++;
      for (int x : graph[node]) {
         if (x == par)
         continue;
         if (!visited.count(x)) {
            dfs(x, node, graph);
            low[node] = min(low[node], low[x]);
            if (disc[node] < low[x]) {
               ret.push_back({ node, x });
            }
         } else{
            low[node] = min(low[node], disc[x]);
         }
      }
   }
   vector<vector<int> > criticalConnections(int n, vector<vector<int> >& v) {
      disc.resize(n + 1);
      low.resize(n + 1);
      time = 0;
      vector<int> graph[n + 1];
      for (int i = 0; i < v.size(); i++) {
         int u = v[i][0];
         int w = v[i][1];
         graph[u].push_back(w);
         graph[w].push_back(u);
      }
      dfs(0, -1, graph);
      return ret;
   }
};
main(){
   Solution ob;
   vector<vector<int>> v = {{0,1},{1,2},{2,0},{1,3}};
   print_vector(ob.criticalConnections(4,v));
}

Đầu vào

4, {{0,1},{1,2},{2,0},{1,3}}

Đầu ra

[[1, 3, ],]