Mô phỏng sóc trong C ++

Có một cái cây, một con sóc và một số loại hạt. Vị trí được biểu thị bằng các ô trong lưới 2D. Mục tiêu của bạn là tìm khoảng cách tối thiểu để con sóc thu thập tất cả các loại hạt và đặt chúng dưới gốc cây từng quả một. Con sóc chỉ có thể lấy nhiều nhất một hạt cùng một lúc và có thể di chuyển theo bốn hướng - lên, xuống, trái và phải, đến ô bên cạnh. Khoảng cách được biểu thị bằng số lần di chuyển.

Vì vậy, nếu đầu vào là Chiều cao:5 Chiều rộng:7 Vị trí cây:[2,2] Sóc:[4,4] Quả hạch:[[3,0], [2,5]], thì đầu ra sẽ là 12 ,

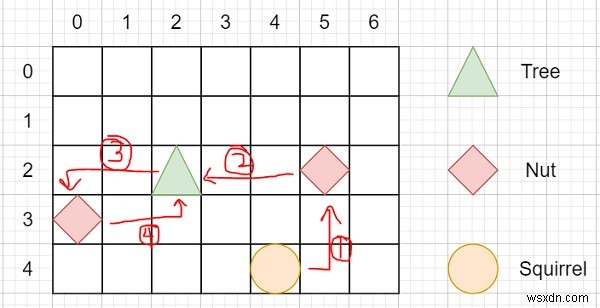
Để giải quyết vấn đề này, chúng tôi sẽ làm theo các bước sau -

• Xác định một hàm calc (), hàm này sẽ nhận x1, y1, x2, y2,

• trả về | x1 - x2 | + | y1 - y2 |

• Xác định một hàm minDistance (), hàm này sẽ lấy chiều cao, chiều rộng, một cây mảng, một sq mảng, một hạt của mảng 2D,

• ret:=0

• maxDiff:=-inf

• để khởi tạo i:=0, khi tôi

  • dist:=calc (cây [0], cây [1], quả hạch [i, 0], quả hạch [i, 1])

  • ret:=ret + 2 * dist

  • maxDiff:=tối đa của maxDiff và 2 * dist - (dist + calc (nut [i, 0], nut [i, 1], sq [0], sq [1]))

• trả về ret - maxDiff

Ví dụ

Hãy cùng chúng tôi xem cách triển khai sau để hiểu rõ hơn -

#include <bits/stdc++.h>
using namespace std;
class Solution {
public:
   int calc(int x1, int y1, int x2, int y2){
      return abs(x1 - x2) + abs(y1 - y2);
   }
   int minDistance(int height, int width, vector<int>& tree, vector<int>& sq, vector<vector>& nuts) {
      int ret = 0;
      int maxDiff = INT_MIN;
      for (int i = 0; i < nuts.size(); i++) {
         int dist = calc(tree[0], tree[1], nuts[i][0],
         nuts[i][1]);
         ret += 2 * dist;
         maxDiff = max(maxDiff, 2 * dist - (dist + calc(nuts[i][0], nuts[i][1], sq[0], sq[1])));
      }
      return ret - maxDiff;
   }
};
main(){
   Solution ob;
   vector<int> v = {2,2}, v1 = {4,4};
   vector<vector<int>> v2 = {{3,0}, {2,5}};
   cout << (ob.minDistance(5,7,v, v1, v2));
}

Đầu vào

5, 7, {2,2},{4,4}, {{3,0}, {2,5}}

Đầu ra

12