Chúng tôi được cung cấp với một ma trận vuông chỉ chứa 0 và 1. 0 đại diện cho một nơi trống trải và 1 có nghĩa là chướng ngại vật. Chúng ta phải tìm một số gương có thể đặt các ô sáng sao cho các gương này có thể truyền ánh sáng từ dưới sang phải. Điều này có thể thực hiện được khi gương được đặt ở chỉ mục [i, j] và đối với tất cả các ô ở bên phải trong hàng cụ thể (i) đó và các ô trong phần tử (j) trong cột cụ thể đó không có chướng ngại vật nào.
Nếu gương ở A [i] [j], thì tất cả A [i + 1 đến n] [j] và A [i] [j + 1 đến n] đều trống, tức là 0. Như thể hiện trong hình bên dưới.
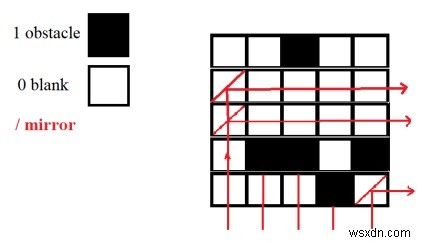
Đầu vào
Arr[][] = {{0,0,1,0,0},{0,0,0,0,0},{0,0,0,0,0},{0,1,1,0,1},{1,1,1,0,1}} Đầu ra
No. of mirrors : 3
Giải thích - Như hình bên. Có thể đặt gương ở các ô
Arr [1] [0] - hàng 1 và cột 0 có tất cả số 0 bên dưới và bên phải của nó.
Arr [2] [0] - hàng 2 và cột 0 có tất cả số 0 bên dưới và bên phải của nó.
Arr [4] [4] - Ô cuối cùng, là 0 và không có hàng nào bên dưới và cột bên phải.
Phương pháp tiếp cận được sử dụng trong chương trình dưới đây như sau
-
Mảng Arr [] [] được sử dụng để biểu diễn ma trận của 0 và 1 ..
-
Hàm MaximumMirror (int mat [] [], int n) nhận ma trận và nó ở phía n làm đầu vào và trả về số lượng các gương tối đa có thể được đặt như hình trên.
-
Cờ biến được sử dụng để đánh dấu sự hiện diện của chướng ngại vật trong các ô bên dưới hoặc các ô bên phải arr [i] [j].
-
Số đếm được sử dụng để biểu thị số lượng gương, ban đầu là 0.
-
Ma trận đảo chiều từ chỉ số 0,0.
-
Đối với mỗi ô nếu nó trống (có thể đặt gương), hãy kiểm tra các ô bên dưới (k =i + 1 đến n-1). Nếu bất kỳ arr [k] [j] nào là chướng ngại vật (giá trị =1) thì ngắt trong khi lặp lại và đánh dấu cờ là 1. Nếu không, hãy tiếp tục kiểm tra các ô ở bên phải (l =j + 1 đến n-1).
-
Đặt cờ trong trường hợp có chướng ngại vật.
-
Sau cả hai vòng lặp while nếu cờ là 0 thì có thể đặt số gia tăng như nhân bản.
-
Trả lại tính là không. trong số các gương có giá trị tối đa.
Ví dụ
// C++ program to find how many mirrors can transfer
// light from bottom to right
#include <bits/stdc++.h>
using namespace std;
// method returns number of mirror which can transfer
// light from bottom to right
int maximumMirror(int mat[5][5], int N){
// to mark that all cells in the right or bottom are 0---no obstacle
int flag=0;
int count=0; //count of mirrors
int i,j,k,l;
//for all cells
for (int i=0; i<N; i++)
for(j=0;j<N;j++){
//check from next column and next row
int k=i+1;
int l=j+1;
if(mat[i][j]==0) //position for mirror{
while(k<N) //check for rows below{
if(mat[k][j]==1) //keeping column fixed, if there is obstacle break{
flag=0; break; }
else
flag=1;
k++;
}
if(flag==1) //if no obstacle in rows then check columns in right
while(l<N) //checking for columns in right{
if(mat[i][l]==1) //keep row fixed, if obstacle break{
flag=0; break;
}
else
flag=1;
l++;
}
if(flag==1) //there is no obstacle for mirror mat[i][j]
count++;
}
}
return count;
}
int main(){
int N = 5;
//matrix where 1 represents obstacle form 5X5 matrix
int mat[5][5] = {{0,0,1,0,0},{0,0,0,0,0},{0,0,0,0,0},{0,1,1,0,1},{1,1,1,0,1}};
cout <<"Maximum mirrors which can transfer light from bottom to right :"<<
maximumMirror(mat, N) << endl;
return 0;
} Đầu ra
Maximum mirrors which can transfer light from bottom to right :3
