Tìm số lượng các số 0 ở cuối trong cơ sở B Biểu diễn của N! sử dụng C ++

Trong bài này, chúng ta sẽ hiểu vấn đề tìm các số không ở cuối của một số N cho trước trong biểu diễn cơ sở B của giai thừa của nó. Ví dụ

Input : N = 7 Base = 2
Output : 4
Explanation : fact(7) = 5040 in base10 and 1001110110000 in base16 having 4 trailing zero.

Input : N = 11 Base = 5
Output : 2
Explanation : fact(11) = 39916800 in base10 and 40204314200 in base16 having 2 trailing zeroes.

Trước tiên, hãy tóm tắt lại quá trình chuyển đổi bất kỳ số thập phân nào từ cơ số này sang cơ số khác. Hãy lấy một ví dụ về chuyển đổi (5040) 10 thành (?) 2

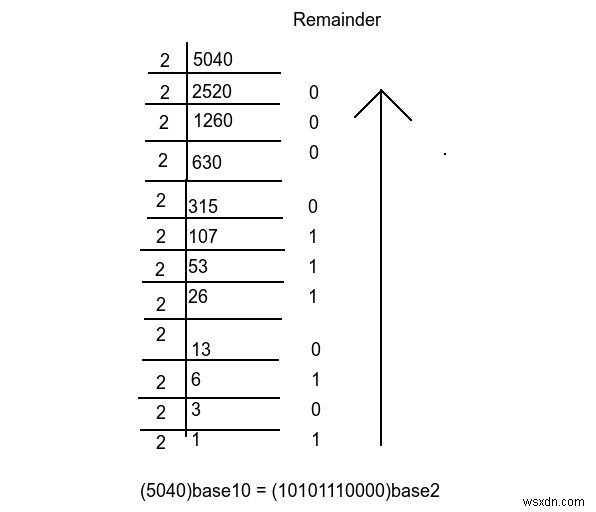
nghĩa là chia số cho 2 và giữ phần dư cho đến khi số đó không thể chia được nữa. Kết quả sẽ là phần còn lại theo thứ tự ngược lại.

Kết quả là chúng ta có 4 số 0 ở cuối và số 0 ở cuối này chúng ta nhận được khi 2 chia số với phần dư là 0.

Thừa số nguyên tố của 5040 =24 * 56711 * 3381 * 181, nghĩa là 2 chia 5040 4 lần với số dư 0 bằng các số 0 ở cuối. Bằng cách này, chúng ta có thể tính toán số lượng các số 0 ở cuối.

Phương pháp tiếp cận để tìm ra giải pháp

Chúng tôi đã thảo luận ở trên về cách tìm số lượng các số 0 ở cuối. Chúng ta cần tìm lũy thừa cao nhất của B theo giai thừa N, giả sử cơ số B =14, thì 14 trong cơ số 14 sẽ được biểu diễn dưới dạng 10, tức là (14) 10 =(10) 14. Nó còn được gọi là công thức của Legendre.

Mã C ++ cho cách tiếp cận trên

Đây là cú pháp C ++ mà chúng ta có thể sử dụng làm đầu vào để giải quyết vấn đề đã cho -

Ví dụ

#include <bits/stdc++.h>
using namespace std;

vector < pair < int, int >> primeFactorsofBase(int Base) {
   // declaring factors to store prime factors
   // along with occurence in factorisation of Base .
   vector < pair < int, int >>factors;

   for (int i = 2; Base != 1; i++) {
      if (Base % i == 0) {
         int count = 0;
         while (Base % i == 0){
            Base = Base / i;
            count++;
         }

         factors.push_back (make_pair (i, count));
      }
   }
   return factors;
}


int main () {
   int N = 11, Base = 5;
   // finding the largest power of Base that divides factorial N.
   vector < pair < int, int >>prime_factors;
   // finding prime factors by primeFactorsofBase() function.
   prime_factors = primeFactorsofBase(Base);

   int result = INT_MAX;
   for (int i = 0; i < prime_factors.size (); i++) {
      // calculating minimum power.
      int count = 0;
      int r = prime_factors[i].first;
      while (r <= N){
         count += (N / r);
         r = r * prime_factors[i].first;
      }
      result = min (result, count / prime_factors[i].second);
   }
   //printing trailing zeroes stored in result.
   cout << "Number of trailing zeroes: " <<result;
   return 0;
}

Đầu ra

Number of trailing zeroes: 2

Giải thích về đoạn mã trên

tìm lũy thừa lớn nhất của Base bằng cách sử dụng một vectơ.
Để tính lũy thừa lớn nhất, hãy tính thừa số nguyên tố bằng cách sử dụng vectơ để lưu trữ tất cả các thừa số nguyên tố.
Sau đó, tính lũy thừa tối thiểu của tất cả các thừa số nguyên tố của Cơ số.
Cuối cùng, in kết quả.

Kết luận

Trong bài viết này, chúng tôi giải quyết vấn đề tìm số lượng các số 0 ở cuối trong biểu diễn cơ sở B của giai thừa N, chúng tôi giải quyết vấn đề này bằng cách sử dụng công thức Legendre. Chúng tôi cũng viết mã C ++ để giải quyết vấn đề tương tự. Bạn có thể viết mã này bằng bất kỳ ngôn ngữ nào khác như Java, C, python, v.v. Chúng tôi hy vọng bạn thấy bài viết này hữu ích.