Trong bài viết này, chúng tôi sẽ giải thích các cách tiếp cận để tìm số lượng các quan hệ phản xạ trên một tập hợp. Trong bài toán này, chúng ta được cho với số n, và trên tập hợp n số tự nhiên, chúng ta phải xác định số quan hệ phản xạ.
Mối quan hệ phản xạ - Một quan hệ trong tập A được gọi là phản xạ nếu (a, a) thuộc R với mọi 'a' thuộc tập A. Ví dụ -
Input : x = 1
Output : 1
Explanation : set = { 1 }, reflexive relations on A * A :
{ { 1 } }
Input : x = 2
Output : 4
Explanation : set = { 1,2 }, reflexive relations on A * A :
{ ( 1, 1 ) , ( 2, 2 ) }
{ ( 1, 1 ), ( 2, 2 ), ( 1, 2 ) }
{ ( 1, 1 ), ( 2, 2 ), ( 1, 2 ), ( 2, 1 ) }
{ ( 1, 1 ), ( 2, 2 ), ( 2, 1 ) } Do đó, một quan hệ là phản xạ nếu:(a, a) ∈ R ∀ a ∈ A.
Phương pháp tiếp cận để tìm giải pháp
Số quan hệ phản xạ này trên một tập phần tử có thể được giải bằng công thức 2n2 − n. Công thức chung này được tạo ra bằng cách tính toán số lượng các quan hệ phản xạ của các số nguyên.
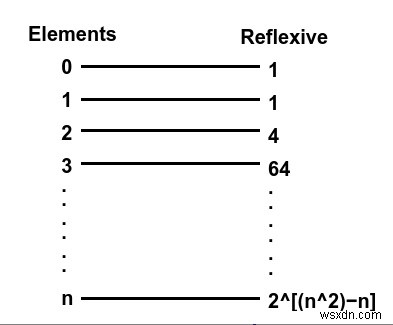
Ví dụ
#include <iostream>
using namespace std;
int countReflexive(int n){
int ans = 1 << (n*n - n);
return ans;
}
int main(){
int n ;
cin >> n ; // taking input n from the user using std cin.
int result = countReflexive(n); // calling function to calculate number of reflexive relations
cout << "Number of reflexive relations on set: " << result ; // printing the answer
return 0;
} Đầu ra
Number of reflexive relations on set: 1
Giải thích về Chương trình trên
Chương trình này rất dễ hiểu vì chúng tôi chỉ lấy dữ liệu đầu vào từ người dùng và đưa nó vào công thức 2n2 − n và chúng tôi đang sử dụng toán tử dịch chuyển trái "<<" để tính toán công thức, Độ phức tạp về thời gian của mã này là O (1) ngày càng chậm khi kích thước của n tăng lên.
Kết luận
Trong bài viết này, chúng tôi giải quyết một vấn đề để tìm Số lượng các mối quan hệ phản xạ trên một tập hợp. Chúng tôi đã thảo luận về cách tiếp cận đơn giản để giải quyết vấn đề đã cho như một công thức để tính số lượng các quan hệ phản xạ được các nhà toán học suy ra.
Chúng tôi cũng đã học chương trình C ++ cho vấn đề này, qua đó chúng tôi đã tìm ra giải pháp với độ phức tạp Thời gian là O (1). Chúng ta có thể viết cùng một chương trình bằng các ngôn ngữ khác như C, java, python và các ngôn ngữ khác.
