Giả sử chúng ta có một cây nhị phân. Một nút được gọi là không đủ nếu mọi đường dẫn từ gốc đến lá giao nhau với nút này có tổng hoàn toàn nhỏ hơn giới hạn. Chúng ta phải xóa đồng thời tất cả các nút không đủ và trả về gốc của cây nhị phân kết quả. Vì vậy, nếu cây giống, và giới hạn là 1 -
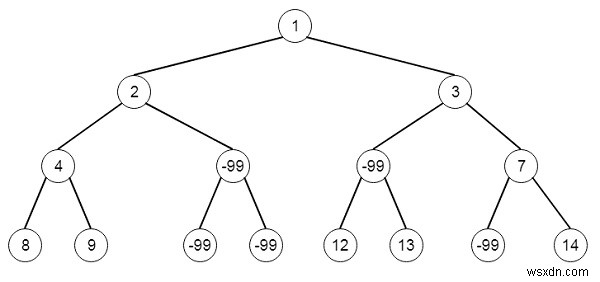
Khi đó cây đầu ra sẽ là -
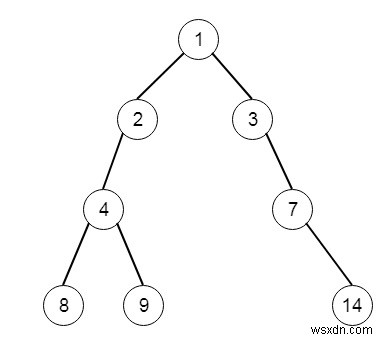
Để giải quyết vấn đề này, chúng tôi sẽ làm theo các bước sau -
- Xác định phương thức giải quyết (), phương thức này sẽ tận gốc và có giới hạn
- nếu nút không có cây con trái và phải, thì
- nếu giá trị của root nhỏ hơn 1, trả về null, nếu không root
- nếu gốc có cây con bên trái, thì bên trái của gốc:=giải quyết (bên trái của gốc, giới hạn - giá trị của gốc)
- nếu gốc có cây con bên phải, thì bên phải của gốc:=giải quyết (quyền của gốc, giới hạn - giá trị của gốc)
- nếu gốc có cây con bên trái hoặc cây con bên phải hoặc cả hai, thì trả về gốc, nếu không thì null.
Hãy cùng chúng tôi xem cách triển khai sau để hiểu rõ hơn -
Ví dụ
class Solution(object): def sufficientSubset(self, root, limit): """ :type root: TreeNode :type limit: int :rtype: TreeNode """ if not root.left and not root.right: return None if root.val<limit else root if root.left: root.left= self.sufficientSubset(root.left,limit-root.val) if root.right: root.right = self.sufficientSubset(root.right,limit-root.val) return root if root.left or root.right else None
Đầu vào
[1,2,3,4,-99,-99,7,8,9,-99,-99,12,13,-99,14] 1
Đầu ra
[1,2,3,4,null,null,7,8,9,null,14]
