Kết nối các thành phố với chi phí tối thiểu bằng Python

Giả sử có N thành phố được đánh số từ 1 đến N. Chúng ta có các kết nối, trong đó mỗi kết nối [i] là [city1, city2, cost] điều này thể hiện chi phí để kết nối city1 và city2 với nhau . Chúng ta phải tìm ra chi phí tối thiểu để đối với mỗi cặp thành phố, tồn tại một con đường kết nối (có thể có độ dài bằng 1) nối hai thành phố đó với nhau. Chi phí là tổng chi phí kết nối được sử dụng. Nếu nhiệm vụ không thể thực hiện được, hãy trả về -1.

Vì vậy, nếu biểu đồ giống như -

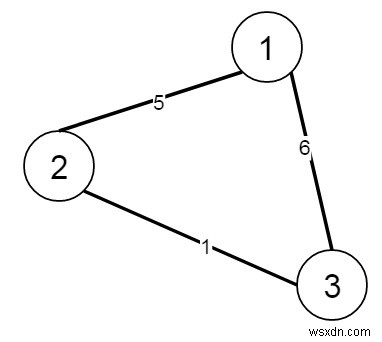
Khi đó đầu ra sẽ là 6, Việc chọn hai thành phố bất kỳ sẽ kết nối tất cả các thành phố, vì vậy chúng tôi chọn tối thiểu 2, [1, 5]

Để giải quyết vấn đề này, chúng tôi sẽ làm theo các bước sau -

• Xác định phương thức được gọi là find (), điều này sẽ mất x

• nếu cha [x] là -1, thì trả về x

• cha [x]:=find (cha [x])

• trả về cha mẹ [x]

• Tạo một phương thức khác được gọi là union (), phương thức này sẽ lấy x và y

• parent_x:=find (x), parent_y:=find (y)

• nếu parent_x =parent_y, thì trả về, nếu không thì parent [parent_y]:=parent_x

• Từ phương thức chính, nó sẽ lấy n và conn

• cha:=một mảng có kích thước n và điền vào giá trị này bằng - 1, đặt disjoint:=n - 1, cost:=0

• c:=danh sách conn được sắp xếp, sắp xếp thứ này dựa trên chi phí

• i:=0

• trong khi i

  • x:=c [i, 0] và y:=c [i, 1]

  • nếu find (x) không giống như find (y), thì hãy giảm disjoint đi 1, tăng chi phí lên c [i, 2] và thực hiện union (x, y)

  • tăng tôi lên 1

• trả về chi phí khi disjoint là 0, nếu không thì trả về -1

Ví dụ (Python)

Hãy cùng chúng tôi xem cách triển khai sau đây để hiểu rõ hơn -

class Solution(object):
   def find(self, x):
      if self.parent[x] == -1:
         return x
      self.parent[x] = self.find(self.parent[x])
      return self.parent[x]
   def union(self,x,y):
      parent_x = self.find(x)
      parent_y = self.find(y)
      if parent_x == parent_y:
         return
      self.parent[parent_y] = parent_x
   def minimumCost(self, n, connections):
      self.parent = [ -1 for i in range(n+1)]
      disjoint = n-1
      cost = 0
      c = sorted(connections,key=lambda v:v[2])
      i = 0
      while i<len(c) and disjoint:
         x = c[i][0]
         y = c[i][1]
         if self.find(x)!=self.find(y):
            disjoint-=1
            cost+=c[i][2]
            self.union(x,y)
            i+=1
         return cost if not disjoint else -1
ob = Solution()
print(ob.minimumCost(3, [[1,2,5], [1,3,6], [2,3,1]]))

Đầu vào

3
[[1,2,5],[1,3,6],[2,3,1]]

Đầu ra

-1