Diện tích tam giác lớn nhất trong Python

Giả sử chúng ta có một danh sách các điểm trên một mặt phẳng. Chúng ta phải tìm diện tích của tam giác lớn nhất có thể được tạo thành bởi 3 điểm bất kỳ.

Vì vậy, nếu đầu vào là [[0,0], [0,1], [1,0], [0,2], [2,0]], thì đầu ra sẽ là 2

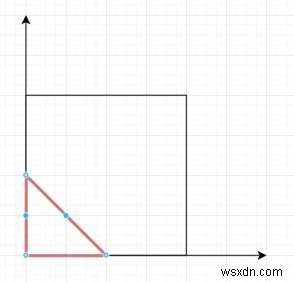
Để giải quyết vấn đề này, chúng tôi sẽ làm theo các bước sau -

• res:=0
• N:=kích thước của danh sách điểm
• đối với tôi trong phạm vi từ 0 đến N - 2, thực hiện
  • đối với j trong phạm vi i + 1 đến N - 1, thực hiện
    • đối với k trong phạm vi i + 2 đến N, thực hiện
      • (x1, y1):=điểm [i],
      • (x2, y2):=điểm [j],
      • (x3, y3):=điểm [k]
      • res:=tối đa của res, 0,5 * | x1 * (y2 - y3) + x2 * (y3 - y1) + x3 * (y1 - y2)
• trả lại res

Hãy cùng chúng tôi xem cách triển khai sau để hiểu rõ hơn -

Ví dụ

class Solution:
   def largestTriangleArea(self, points):
      res = 0
      N = len(points)
      for i in range(N - 2):
         for j in range(i + 1, N - 1):
            for k in range(i + 2, N):
               (x1, y1), (x2, y2), (x3, y3) = points[i],points[j],points[k]
               res = max(res, 0.5 * abs(x1 * (y2 - y3) + x2 * (y3 - y1) + x3 * (y1 - y2)))
      return res
ob = Solution()
print(ob.largestTriangleArea([[0,0],[0,1],[1,0],[0,2],[2,0]]))

Đầu vào

[[0,0],[0,1],[1,0],[0,2],[2,0]]

Đầu ra

2.0