Giả sử chúng ta có một đồ thị dưới dạng biểu diễn danh sách kề, chúng ta phải tìm ma trận 2D M ở đâu
-
M [i, j] =1 khi có một đường đi giữa các đỉnh i và j.
-
M [i, j] =0 nếu không.
Vì vậy, nếu đầu vào giống như
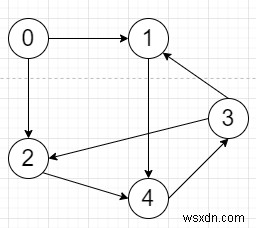
thì đầu ra sẽ là
| 1 | 1 | 1 | 1 | 1 |
| 0 | 1 | 1 | 1 | 1 |
| 0 | 1 | 1 | 1 | 1 |
| 0 | 1 | 1 | 1 | 1 |
| 0 | 1 | 1 | 1 | 1 |
Để giải quyết vấn đề này, chúng tôi sẽ làm theo các bước sau -
-
ans:=ma trận 2d kích thước n x n, trong đó n là số đỉnh, điền các số 0
-
đối với tôi trong phạm vi từ 0 đến n, hãy thực hiện
-
q:=một hàng đợi, và chèn tôi vào lúc đầu
-
trong khi q không trống, thực hiện
-
node:=phần tử đầu tiên của q và xóa phần tử đầu tiên khỏi q
-
nếu ans [i, node] khác 0 thì
-
chuyển sang lần lặp tiếp theo
-
-
ans [i, node]:=1
-
hàng xóm:=graph [node]
-
đối với mỗi n trong hàng xóm, hãy làm
-
chèn n vào cuối q
-
-
-
-
trả lại ans
Hãy cùng chúng tôi xem cách triển khai sau để hiểu rõ hơn -
Ví dụ
class Solution: def solve(self, graph): ans=[[0 for _ in graph] for _ in graph] for i in range(len(graph)): q=[i] while q: node=q.pop(0) if ans[i][node]: continue ans[i][node]=1 neighbors=graph[node] for n in neighbors: q.append(n) return ans ob = Solution() adj_list = [[1,2],[4],[4],[1,2],[3]] priunt(ob.solve(adj_list))
Đầu vào
[[1,2],[4],[4],[1,2],[3]]
Đầu ra
[[1, 1, 1, 1, 1], [0, 1, 1, 1, 1], [0, 1, 1, 1, 1], [0, 1, 1, 1, 1], [0, 1, 1, 1, 1] ]
