Giả sử chúng ta có một lưới nước vô hạn. Chúng ta có thể thêm từng khối đất vào lưới đó lần lượt. Chúng ta có một danh sách các tọa độ được gọi là land_requests trong đó mỗi tọa độ có dạng [r, c] trong đó r là hàng và c là cột. Chúng tôi phải tìm một danh sách trong đó mỗi phần tử đại diện cho số lượng các hòn đảo tồn tại sau khi thêm từng khối đất từ land_requests.
Vì vậy, nếu đầu vào giống như land_requests =[[1, 1], [2, 4], [1, 2], [1, 4], [1, 3]], thì đầu ra sẽ là [1, 2 , 2, 2, 1] as
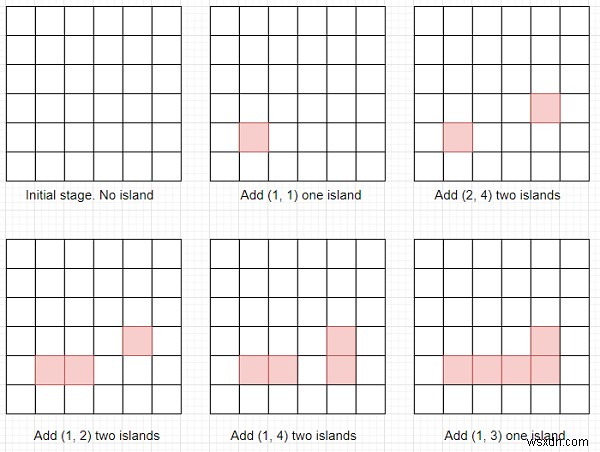
Để giải quyết vấn đề này, chúng tôi sẽ làm theo các bước sau -
-
d:=danh sách các hướng như [(−1, 0), (0, 1), (1, 0), (0, −1)]
-
idx:=0
-
mp:=một bản đồ mới
-
p:=một danh sách mới
-
size:=a new list
-
comp:=0
-
ans:=một danh sách mới
-
Xác định một hàm tìm kiếm (). Điều này sẽ mất bạn
-
nếu u giống với p [u] thì
-
trả lại bạn
-
p [u]:=search (p [u])
-
-
trả lại p [u]
-
Xác định một hàm kết nối (). Điều này sẽ mất bạn, v
-
pu:=search (u), pv:=search (v)
-
nếu pu giống với pv thì
-
trở lại
-
-
comp:=comp - 1
-
nếu size [pu]> =size [pv] thì
-
p [pv]:=pu
-
size [pu]:=size [pu] + size [pv]
-
-
nếu không,
-
p [pu]:=pv
-
size [pv]:=size [pv] + size [pu]
-
-
Từ phương thức chính, hãy làm như sau -
-
đối với mỗi yêu cầu trong land_requests, hãy thực hiện
-
(i, j):=request
-
mp [i, j]:=idx
-
chèn idx vào cuối p
-
chèn 1 vào cuối kích thước
-
idx:=idx + 1
-
comp:=comp + 1
-
với mỗi k trong d, làm
-
ni:=i + k [1]
-
nj:=j + k [0]
-
nếu (ni, nj) ở trong mp, thì
-
kết nối (mp [(i, j)], mp [(ni, nj)])
-
-
-
chèn comp vào cuối ans
-
-
trả lại ans
Hãy cùng chúng tôi xem cách triển khai sau để hiểu rõ hơn -
Ví dụ
d = [(−1, 0), (0, 1), (1, 0), (0, −1)] class Solution: def search(self, u): if u == self.p[u]: return u self.p[u] = self.search(self.p[u]) return self.p[u] def connect(self, u, v): pu = self.search(u) pv = self.search(v) if pu == pv: return self.comp −= 1 if self.size[pu] >= self.size[pv]: self.p[pv] = pu self.size[pu] += self.size[pv] else: self.p[pu] = pv self.size[pv] += self.size[pu] def solve(self, land_requests): self.idx = 0 self.mp = dict() self.p = [] self.size = [] self.comp = 0 ans = [] for request in land_requests: i, j = request self.mp[(i, j)] = self.idx self.p.append(self.idx) self.size.append(1) self.idx += 1 self.comp += 1 for k in d: ni = i + k[1] nj = j + k[0] if (ni, nj) in self.mp: self.connect(self.mp[(i, j)], self.mp[(ni, nj)]) ans.append(self.comp) return ans ob = Solution() land_requests = [[1, 1],[2, 4],[1, 2],[1, 4],[1, 3]] print(ob.solve(land_requests))
Đầu vào
[[1, 1],[2, 4],[1, 2],[1, 4],[1, 3]]
Đầu ra
[1, 2, 2, 2, 1]
