Chương trình tìm điểm gần nhất có cùng tọa độ x hoặc y bằng Python

Giả sử chúng ta có một tập hợp các điểm được cho trong một mảng được gọi là pts. Chúng tôi cũng có một điểm khác (x, y) là vị trí hiện tại của chúng tôi. Chúng tôi đang xác định một điểm hợp lệ là, một điểm có cùng tọa độ x hoặc cùng tọa độ y với điểm hiện tại của chúng tôi. Chúng ta phải trả về chỉ số của điểm hợp lệ có khoảng cách Manhattan nhỏ nhất từ ​​vị trí hiện tại của chúng ta (x, y). Nếu có nhiều hơn một điểm thì trả về điểm hợp lệ có chỉ số nhỏ nhất. (Lưu ý:khoảng cách Manhattan giữa hai điểm (a, b) và (p, q) là | a - p | + | b - q |.

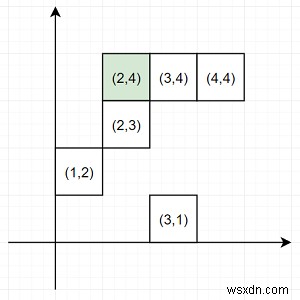
Vì vậy, nếu đầu vào giống như pts =[(1,2), (3,1), (3,4), (2,3), (4,4)] pt =(2,4), thì đầu ra sẽ là 2 vì có hai điểm gần nhất (3,4) và (2,3), nhưng chỉ số của (3,4) nhỏ hơn.

Để giải quyết vấn đề này, chúng tôi sẽ làm theo các bước sau -

• x, y:=pt

• idx:=-1

• nhỏ nhất:=infinity

• đối với mỗi p tính bằng pts, hãy thực hiện

  • nếu p [0] giống x hoặc p [1] giống y, thì

    • dist:=| x - p [0] | + | y ​​- p [1] |

    • nếu dist

      • idx:=chỉ số của p tính bằng pts

      • nhỏ nhất:=dist

    • ngược lại khi dist bằng nhỏ nhất thì

      • nếu chỉ mục của p trong pts

        • idx:=chỉ số của p tính bằng pts

        • nhỏ nhất:=dist

• trả về idx

Hãy cùng chúng tôi xem cách triển khai sau để hiểu rõ hơn -

Ví dụ

def solve(pts, pt):
   x, y = pt
   idx = -1
   smallest = float("inf")
   for p in pts:
      if p[0] == x or p[1] == y:
         dist = abs(x - p[0]) + abs(y - p[1])
         if dist < smallest:
            idx = pts.index(p)
            smallest = dist
         elif dist == smallest:
            if pts.index(p) < idx:
               idx = pts.index(p)
               smallest = dist
   return idx
pts = [(1,2),(3,1),(3,4),(2,3),(4,4)]
pt = (2,4)
print(solve(pts, pt))

Đầu vào

[(1,2),(3,1),(3,4),(2,3),(4,4)], (2,4)

Đầu ra

2