Chương trình tìm đường dẫn với xác suất tối đa bằng Python

Giả sử chúng ta có một đồ thị có trọng số vô hướng với n nút (các nút được đánh số từ 0 trở đi), Đồ thị này được đưa ra làm đầu vào bằng cách sử dụng danh sách cạnh, đối với mỗi cạnh e, nó có xác suất thành công của việc vượt qua xác suất cạnh đó [e]. Chúng ta cũng có các nút bắt đầu và kết thúc, chúng ta phải tìm ra con đường có xác suất thành công tối đa để đi từ đầu đến cuối và trả về xác suất thành công của nó. Nếu chúng tôi không thể tìm thấy bất kỳ đường dẫn nào, hãy trả về 0.

Vì vậy, nếu đầu vào giống như

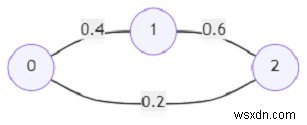
thì đầu ra sẽ là 0,24 vì có hai đường đi từ nút 0 đến 2, một đường dẫn có xác suất 0,2, đường khác qua nút 1 có xác suất 0,4 * 0,6 =0,24, đây là mức tối đa.

Để giải quyết vấn đề này, chúng tôi sẽ làm theo các bước sau -

• g:=tạo đồ thị từ danh sách cạnh đã cho và sử dụng giá trị xác suất làm trọng số

• q:=một cấu trúc dữ liệu hàng đợi

• insert (start, 1) vào q

• đã thăm:=một bản đồ để giữ nút đã truy cập

• trong khi q không trống, thực hiện

  • (node, prob):=mục đầu tiên của q và xóa nó khỏi q

  • nếu đã truy cập [node]> prob thì

    • chuyển sang lần lặp tiếp theo

  • nếu không,

    • đã ghé thăm [node]:=prob

  • đối với mỗi điều chỉnh nút liền kề và xác suất nextProb trong g [nút], thực hiện

    • nếu đã truy cập [adj]

      • insert (adj, prob * nextProb) vào cuối q

• trở lại đã thăm [end]

Hãy cùng chúng tôi xem cách triển khai sau để hiểu rõ hơn -

Ví dụ

from collections import defaultdict, deque
def solve(edges, probability, start, end):
   g = defaultdict(list)
   for i in range(len(edges)):
      src, dst = edges[i][0], edges[i][1]
      prob = probability[i]
      g[src].append((dst, prob))
      g[dst].append((src, prob))
   q = deque()
   q.append((start, 1))
   visited = defaultdict(int)
   while q:
      node, prob = q.popleft()
      if visited[node] > prob:
         continue
      else:
         visited[node] = prob
      for adj, nextProb in g[node]:
         if visited[adj] < prob * nextProb:
            q.append((adj, prob * nextProb))
   return visited[end]
edges = [[0,1],[1,2],[0,2]]
probability = [0.5,0.5,0.2]
start = 0
end = 2
print(solve(edges, probability, start, end))

Đầu vào

[[0,1],[1,2],[0,2]], [0.5,0.5,0.2], 0, 2

Đầu ra

0.25