Computer >> Máy Tính >  >> Lập trình >> Python

Chương trình tính số học kỳ tối thiểu để bao gồm tất cả các khóa học khác nhau bằng Python

Giả sử chúng ta có một số n, chỉ ra rằng có n khóa học khác nhau có nhãn từ 1 đến n. Chúng ta cũng có một mảng được gọi là quan hệ trong đó các quan hệ [i] chứa một cặp (presCourse_i, nextCourse_i), đại diện cho mối quan hệ điều kiện tiên quyết giữa khóa học presCourse_i và khóa học nextCourse_i:vì vậy khóa học trước khóa học nextCourse_i phải được thực hiện trước khóa học nextCourse_i. Và tham số cuối cùng chúng ta có đó là k. Trong một học kỳ, chúng ta có thể tham gia nhiều nhất k số môn học miễn là chúng ta đã thực hiện tất cả các điều kiện tiên quyết trong học kỳ trước cho các môn học chúng ta đang tham gia. Chúng tôi phải tìm số học kỳ tối thiểu cần thiết để tham gia tất cả các khóa học.

Vì vậy, nếu đầu vào giống như

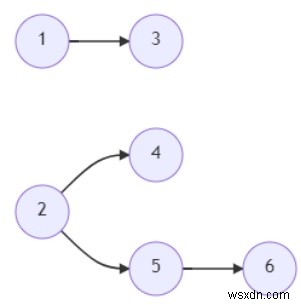
Chương trình tính số học kỳ tối thiểu để bao gồm tất cả các khóa học khác nhau bằng Python

thì đầu ra sẽ là 3 vì trong học kỳ đầu tiên chúng ta có thể học khóa 1 và 2, bây giờ chúng ta đủ điều kiện cho khóa 3, 4 và 5, vì vậy nếu chúng ta thi 5 và bất kỳ một trong 3 hoặc 4 cho học kỳ hai, thì chúng ta có thể kết thúc tất cả các khóa học trong học kỳ tiếp theo. Vì vậy, chúng tôi cần tổng cộng 3 học kỳ

Để giải quyết vấn đề này, chúng tôi sẽ làm theo các bước sau -

  • đã lấy:=một tập hợp mới

  • g1:=một danh sách có n danh sách trống

  • g2:=một danh sách mới có kích thước n và điền bằng 0

  • w:=một danh sách mới có kích thước n và điền bằng 0

  • học kỳ:=0

  • đối với mỗi x trong quan hệ, thực hiện

    • chèn x [0] -1 vào cuối g1 [x [1] -1]

    • chèn x [1] -1 vào cuối g2 [x [0] -1]

  • weight:=một danh sách mới từ độ dài của tất cả các mục trong g1

  • đối với tôi trong phạm vi từ 0 đến n - 1, hãy thực hiện

    • đối với mỗi x trong g1 [i], thực hiện

      • w [x]:=tối đa của w [x] và trọng lượng [i]

  • trong khi kích thước của lấy

    • các khóa học:=một danh sách mới

    • đối với tôi trong phạm vi từ 0 đến n - 1, hãy thực hiện

      • nếu g1 [i] trống và tôi không được lấy, thì

        • insert (i, w [i]) vào cuối khóa học

      • nếu kích thước của các khóa học> k, thì

        • Course =sắp xếp các khóa học dựa trên tham số thứ hai theo thứ tự ngược lại

        • các khóa học:=danh sách k khóa học đầu tiên

      • học kỳ:=học kỳ + 1

      • đối với mỗi x trong các khóa học, hãy thực hiện

        • đối với mỗi y trong g2 [x [0]], hãy thực hiện

          • xóa x [0] khỏi g1 [y]

        • g2 [x [0]]:=danh sách trống

        • chèn x [0] vào lấy

  • học kỳ trở lại

Ví dụ

Hãy cùng chúng tôi xem cách triển khai sau để hiểu rõ hơn 

def solve(n, relations, k):
   taken = set()
   g1 = [[] for _ in range(n)]
   g2 = [[] for _ in range(n)]
   w = [0] * n
   semester = 0
   for x in relations:
      g1[x[1]-1].append(x[0]-1)
      g2[x[0]-1].append(x[1]-1)

   weight = list(map(len, g1))
   for i in range(n):
      for x in g1[i]:
         w[x] = max(w[x], weight[i])


   while len(taken) < n:
      courses = []
      for i in range(n):
         if (not g1[i]) and (i not in taken):
            courses.append([i,w[i]])
      if len(courses) > k:
         courses = sorted(courses, key = lambda x:x[1],reverse=True)
         courses = courses[:k]

      semester += 1

      for x in courses:
         for y in g2[x[0]]:
            g1[y].remove(x[0])
         g2[x[0]] = []
         taken.add(x[0])
   return semester

n = 6
relations = [(1,3),(2,5),(2,4),(5,6)]
k = 2
print(solve(n, relations, k))

Đầu vào 

6, [(1,3),(2,5),(2,4),(5,6)], 2

Đầu ra 

3