Giả sử chúng ta có một danh sách các vị trí, trong đó có một danh sách các điểm tọa độ nơi có một số ngôi nhà. Nếu bạn muốn tạo một trung tâm dịch vụ tại (xc, yc) sao cho tổng khoảng cách Euclide từ bất kỳ điểm đã cho nào đến (xc, yc) là nhỏ nhất. Vì vậy, chúng ta phải tìm tổng khoảng cách tối thiểu.
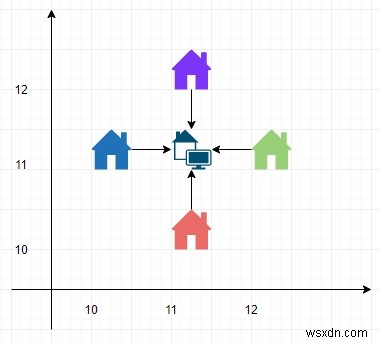
Vì vậy, nếu đầu vào giống như các vị trí =[(10,11), (11,10), (11,12), (12,11)], thì đầu ra sẽ là 4,0
Để giải quyết vấn đề này, chúng tôi sẽ làm theo các bước sau -
-
numIter:=50
-
Xác định một hàm tổng (). Điều này sẽ chiếm cx, cy, vị trí
-
tổng:=0,0
-
đối với mỗi p trong các vị trí, hãy thực hiện
-
x, y:=p
-
tổng:=tổng + Khoảng cách Euclide giữa (cx, cy) và (x, y)
-
-
tổng trả lại
-
Định nghĩa một hàm fy (). Điều này sẽ lấy x, vị trí
-
l:=0, r:=101
-
res:=0
-
đối với tôi trong phạm vi từ 0 đến numIter, thực hiện
-
y1:=l + (r - l) / 3
-
y2:=r - (r - l) / 3
-
t1:=tổng (x, y1, vị trí)
-
t2:=tổng (x, y2, vị trí)
-
res:=tối thiểu của t1 và t2
-
nếu t1
-
r:=y2
-
-
nếu không,
-
l:=y1
-
-
trả lại res
-
Định nghĩa một hàm fx (). Điều này sẽ có các vị trí
-
l:=0, r:=101
-
res:=0
-
đối với tôi trong phạm vi từ 0 đến numIter, thực hiện
-
x1:=l + (r - l) / 3
-
x2:=r - (r - l) / 3
-
t1:=fy (x1, vị trí)
-
t2:=fy (x2, vị trí)
-
res:=tối thiểu của t1 và t2
-
nếu t1
-
r:=x2
-
-
nếu không,
-
l:=x1
-
-
-
trả lại res
-
Từ phương thức chính, trả về fx (vị trí)
Ví dụ
Hãy cùng chúng tôi xem cách triển khai sau đây để hiểu rõ hơn
from math import sqrt
def solve(points):
numIter = 50
def total(cx, cy, positions):
total = 0.0
for p in positions:
x, y = p
total += sqrt((cx - x) * (cx - x) + (cy - y) * (cy - y))
return total
def fy(x, positions):
l, r = 0, 101
res = 0
for i in range(numIter):
y1 = l + (r - l) / 3
y2 = r - (r - l) / 3
t1 = total(x, y1, positions)
t2 = total(x, y2, positions)
res = min(t1, t2)
if t1 < t2:
r = y2
else:
l = y1
return res
def fx(positions):
l, r = 0, 101
res = 0
for i in range(numIter):
x1 = l + (r - l) / 3
x2 = r - (r - l) / 3
t1 = fy(x1, positions)
t2 = fy(x2, positions)
res = min(t1, t2)
if t1 < t2:
r = x2
else:
l = x1
return res
return fx(positions)
positions = [(10,11),(11,10),(11,12),(12,11)]
print(solve(positions)) Đầu vào
[(10,11),(11,10),(11,12),(12,11)]
Đầu ra
4.0
