Chương trình tìm số lượng đường dẫn bị hạn chế từ nút đầu tiên đến nút cuối cùng trong Python

Giả sử chúng ta có một đồ thị liên thông có trọng số vô hướng. Đồ thị có n nút và chúng được đánh dấu từ 1 đến n. Một đường dẫn từ đầu đến cuối là một chuỗi các nút như [z0, z1, z2, ..., zk] ở đây z0 là nút bắt đầu và zk là nút kết thúc và có một cạnh giữa zi và zi + 1 trong đó 0 <=i <=k-1. Khoảng cách của một đường dẫn là tổng các giá trị trọng số trên các cạnh của đường dẫn. Gọi dist (x) là khoảng cách ngắn nhất từ ​​nút n và nút x. Đường bị hạn chế là đường đặc biệt cũng thỏa mãn điều đó dist (zi)> dist (zi + 1) trong đó 0 <=i <=k-1. Vì vậy, chúng ta phải tìm số đường đi bị hạn chế từ nút 1 đến nút n. Nếu câu trả lời quá lớn thì trả về câu trả lời modulo 10 ^ 9 + 7.

Vì vậy, nếu đầu vào giống như

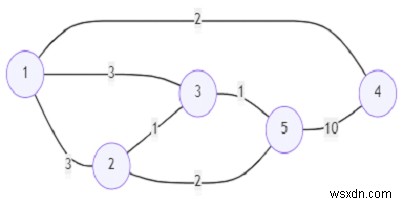
thì đầu ra sẽ là 3 vì có ba đường dẫn bị hạn chế (1,2,5), (1,2,3,5), (1,3,5).

Để giải quyết vấn đề này, chúng tôi sẽ làm theo các bước sau -

• graph:=danh sách kề của biểu đồ được tạo từ danh sách cạnh đã cho

• path:=một mảng có kích thước (n + 1) và được lấp đầy bởi 0

• đường dẫn [n]:=1

• dists:=một mảng có kích thước (n + 1) và được lấp đầy bởi -1

• q:=a queue và insert (0, n) lúc đầu

• trong khi q không trống, thực hiện

  • (dist, node):=phần tử phía trước của q và xóa nó khỏi q

  • nếu dists [node] không giống -1, thì

    • chuyển sang lần lặp tiếp theo

  • dists [node]:=dist

  • đối với mỗi nút lân cận v và trọng số w của biểu đồ [nút], thực hiện

    • nếu dists [v] giống -1 thì

      • chèn (dist + w, v) vào q

    • ngược lại khi dists [v]

      • đường dẫn [nút]:=đường dẫn [nút] + đường dẫn [v]

  • nếu nút giống 1, thì

    • đường dẫn trả về [node] mod 10 ^ 9 + 7

• trả về 0

Ví dụ

Hãy cùng chúng tôi xem cách triển khai sau để hiểu rõ hơn -

from collections import defaultdict
from heapq import heappop, heappush
def solve(n, edges):
   graph = defaultdict(dict)
   for u, v, w in edges:
      graph[u][v] = w
      graph[v][u] = w

   paths = [0] * (n+1)
   paths[n] = 1
   dists = [-1] * (n+1)
   q = [(0, n)]

   while q:
      dist, node = heappop(q)
      if dists[node] != -1:
         continue

      dists[node] = dist
      for v, w in graph[node].items():
         if dists[v] == -1:
            heappush(q, (dist + w, v))
         elif dists[v] < dists[node]:
            paths[node] += paths[v]

      if node == 1:
         return paths[node] % (10**9 + 7)

   return 0

n = 5
edges = [(1,2,3),(1,3,3),(2,3,1),(1,4,2),(5,2,2),(3,5,1),(5,4,10)]
print(solve(n, edges))

Đầu vào

5,[(1,2,3),(1,3,3),(2,3,1),(1,4,2),(5,2,2),(3,5,1),(5,4,10)]

Đầu ra

3