Chương trình kiểm tra sự tồn tại của các đường dẫn giới hạn độ dài cạnh trong Python

Giả sử chúng ta có một đồ thị có trọng số vô hướng với n nút sử dụng một edgeList, trong đó edgeList [i] có ba tham số (u, v, w) biểu thị có một đường đi từ u đến v có khoảng cách là w. Chúng ta cũng có một mảng truy vấn khác trong đó truy vấn [i] có (p, q, lim). Truy vấn này đang cố gắng hỏi liệu có một đường dẫn (trực tiếp hoặc qua một số nút khác) từ p đến q có khoảng cách nhỏ hơn lim hay không. Chúng ta phải trả về một mảng chứa các kết quả Đúng / Sai cho mỗi truy vấn.

Vì vậy, nếu đầu vào giống như

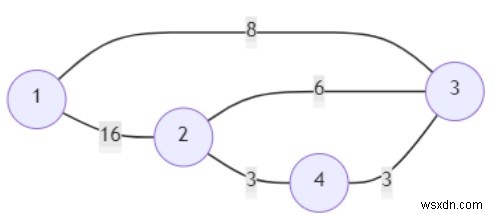
thì đầu ra sẽ là [True, False, True]. Bởi vì để đi từ 1 đến 4, chúng ta có thể đi theo con đường 1 -> 3 -> 4 với chi phí 11, con đường thứ hai là sai vì chúng ta không thể đi từ 2 đến 3 bằng cách sử dụng ít hơn 3, và con đường cuối cùng đúng vì chúng ta có thể đi từ 1 đến 2 bằng cách sử dụng đường dẫn 1 -> 3 -> 2 với chi phí 14 là nhỏ hơn 15.

Để giải quyết vấn đề này, chúng tôi sẽ làm theo các bước sau -

• cha mẹ:=một danh sách từ 0 đến n

• rank:=danh sách có kích thước n + 1 và điền bằng 0

• Định nghĩa một hàm find (). Điều này sẽ đưa cha mẹ, x

• nếu cha [x] giống với x thì

  • trả lại x

• cha [x]:=find (cha, cha [x])

• trả về cha mẹ [x]

• Định nghĩa một hàm union (). Điều này sẽ lấy cha mẹ, a, b

• a:=find (cha, a)

• b:=find (cha, b)

• nếu a giống với b thì

  • trở lại

• nếu xếp hạng [a]

  • cha [a]:=b

• ngược lại khi xếp hạng [a]> xếp hạng [b] thì

  • cha [b]:=a

• nếu không,

  • cha [b]:=a

  • rank [a]:=rank [a] + 1

• Từ phương thức chính, hãy làm như sau -

• sắp xếp edgeList dựa trên thông số trọng lượng

• res:=một mảng có số lượng truy vấn và điền bằng 0

• truy vấn:=danh sách các cặp (i, ch) cho mỗi chỉ mục i và giá trị ch từ các truy vấn

• sắp xếp các truy vấn dựa trên các tham số giới hạn

• ind:=0

• đối với mỗi chỉ mục tôi ba lần (a, b, w) trong các truy vấn, thực hiện

  • while ind

    • union (cha, edgeList [ind, 0])

    • ind:=ind + 1

  • res [i]:=find (cha, a) giống như find (cha, b)

• trả lại res

Ví dụ

Hãy cùng chúng tôi xem cách triển khai sau để hiểu rõ hơn

def solve(n, edgeList, queries):
   parent = [i for i in range(n+1)]

   rank = [0 for i in range(n+1)]

   def find(parent, x):

      if parent[x] == x:
         return x
      parent[x] = find(parent, parent[x])
      return parent[x]

   def union(parent, a, b):

      a = find(parent, a)
      b = find(parent, b)

      if a == b:
         return

      if rank[a] < rank[b]:
         parent[a] = b
      elif rank[a] > rank[b]:
         parent[b] = a
      else:
         parent[b] = a
         rank[a] += 1

   edgeList.sort(key = lambda x: x[2])
   res = [0] * len(queries)
   queries = [[i, ch] for i, ch in enumerate(queries)]
   queries.sort(key = lambda x: x[1][2])

   ind = 0
   for i, (a, b, w) in queries:

      while ind < len(edgeList) and edgeList[ind][2] < w:
         union(parent, edgeList[ind][0], edgeList[ind][1])
         ind += 1

      res[i] = find(parent, a) == find(parent, b)
   return res

n = 4
edgeList = [(1,2,16),(1,3,8),(2,4,3),(2,3,6),(4,3,3),]
queries = [(1,4,12),(2,3,3),(1,2,15)]
print(solve(n, edgeList, queries))

Đầu vào

4, [(1,2,16),(1,3,8),(2,4,3),(2,3,6),(4,3,3)],[(1,4,12),(2,3,3),(1,2,15)]

Đầu ra

[True, False, True]