Chương trình tìm chiều cao tòa nhà tối đa bằng Python

Giả sử chúng ta có một giá trị n và một danh sách các cặp khác được gọi là các giới hạn. Chúng tôi muốn xây dựng n tòa nhà mới trong một thành phố. Nhưng có một số hạn chế. Chúng ta có thể xây dựng trong một dòng và các tòa nhà được dán nhãn từ 1 đến n. Các giới hạn có hai tham số, do đó, các hạn chế [i] =(id_i, max_height_i) cho biết id_i phải có chiều cao nhỏ hơn hoặc bằng max_height_i. Các giới hạn của thành phố về chiều cao của các tòa nhà mới như sau -

Chiều cao của mỗi tòa nhà phải bằng 0 hoặc các giá trị dương.
Chiều cao của tòa nhà đầu tiên phải bằng 0.
Chênh lệch giữa chiều cao bất kỳ của hai tòa nhà liền kề không được vượt quá 1.

Chúng tôi phải tìm chiều cao tối đa có thể của tòa nhà cao nhất.

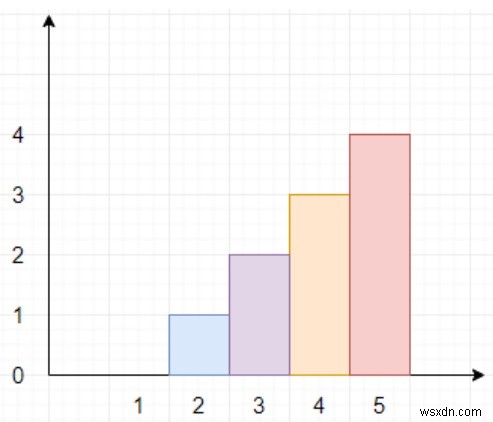
Vì vậy, nếu đầu vào là n =5, các giới hạn =[[2,1], [4,3]], thì đầu ra sẽ là 4 vì chúng ta phải tìm chiều cao tối đa có thể, vì vậy nó có thể là 4 như được hiển thị trong sơ đồ.

Để giải quyết vấn đề này, chúng tôi sẽ làm theo các bước sau -

nếu các giới hạn trống, thì
- trả về n-1
resi:=sắp xếp các hạn chế danh sách dựa trên id
k:=0
idx:=1
đối với mỗi re trong resi, hãy thực hiện
- re [1]:=tối thiểu re [1] và (k + re [0] -idx)
- k:=re [1]
- idx:=re [0]
k:=chiều cao tối đa của phần tử cuối cùng trong resi
idx:=id của phần tử cuối cùng trong resi
đảo ngược resi danh sách
đối với mỗi re trong resi từ mục đầu tiên trở đi, hãy thực hiện
- re [1]:=tối thiểu re [1] và (k-re [0] + idx)
- k:=re [1]
- idx:=re [0]
đảo ngược resi danh sách
f:=0
idx:=1
res:=0
đối với mỗi re trong resi, hãy thực hiện
- ff:=tối thiểu của (f + re [0] -idx) và re [1]
- res:=tối đa của res và thương số của (re [0] - idx + f + ff) / 2
- idx:=re [0]
- f:=ff
trả về tối đa (f + n-idx) và res

Ví dụ

Hãy cùng chúng tôi xem cách triển khai sau để hiểu rõ hơn

def solve(n, restrictions):
   if not restrictions:
      return n-1
   resi = sorted(restrictions, key = lambda x:x[0])

   k = 0
   idx = 1
   for re in resi:
      re[1] = min(re[1], k+re[0]-idx)
      k = re[1]
      idx = re[0]
   k = resi[-1][1]
   idx = resi[-1][0]
   resi.reverse()
   for re in resi[1:]:
      re[1] = min(re[1], k-re[0]+idx)
      k = re[1]
      idx = re[0]
   resi.reverse()

   f = 0
   idx = 1
   res = 0
   for re in resi:
      ff = min(f+re[0]-idx, re[1])
      res = max(res, (re[0] - idx + f + ff) // 2)
      idx = re[0]
      f = ff
   return max(f+n-idx,res)

n = 5
restrictions = [[2,1],[4,3]]
print(solve(n, restrictions))

Đầu vào

5, [[2,1],[4,3]]

Chương trình tìm chiều cao tòa nhà tối đa bằng Python

Ví dụ

Đầu vào

Đầu ra