Computer >> Máy Tính >  >> Lập trình >> Python

Chương trình đếm số tam giác cân từ đa giác đều đỉnh màu trong Python

Giả sử chúng ta có một đa giác đều với n cạnh được biểu diễn dưới dạng một chuỗi nhị phân kích thước n. Các đỉnh có thể được tô màu xanh lam (0) hoặc đỏ (1). Chúng được tô màu theo chiều kim đồng hồ Chúng ta phải đếm số tam giác cân có đỉnh là đỉnh của đa giác đều và màu của chúng giống nhau.

Vì vậy, nếu đầu vào giống như polygon ="111010", thì đầu ra sẽ là 2 vì

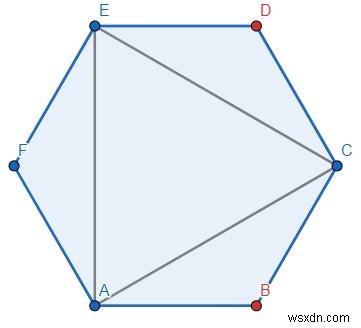
Chương trình đếm số tam giác cân từ đa giác đều đỉnh màu trong Python

có hai tam giác ACE và AFE.

Để giải quyết vấn đề này, chúng tôi sẽ làm theo các bước sau -

  • Xác định một hàm all (). Điều này sẽ mất n
  • nếu n mod 2 giống với 1 thì no:=n * (n-1) / 2
  • nếu không, không:=n * (n / 2-1)
  • nếu n mod 3 giống 0, thì no:=no - n / 3 * 2
  • trả lại không
  • Xác định một hàm non (). Điều này sẽ mất a, n
  • nếu n mod 2 giống với 1, thì
    • s0:=0, s1:=0
    • i:=0
    • while i
    • nếu [i] giống với '0' thì s0:=s0 + 1
    • nếu không thì s1:=s1 + 1
    • i:=i + 1
  • s:=s0 * s1 * 6
  • nếu n mod 3 giống 0, thì
    • n1:=n / 3
    • n2:=n1 * 2
    • i:=0
    • while i
    • nếu a [i] không giống với [(i + n1) mod n], thì
      • s:=s - 2
    • nếu a [i] không giống với [(i + n2) mod n], thì
      • s:=s - 2
    • i:=i + 1
  • nếu không,
    • s00:=0, s01:=0, s10:=0, s11:=0, s:=0
    • i:=0
    • while i
    • nếu [i] giống với '0' thì s00:=s00 + 1
    • nếu không thì s01:=s01 + 1
    • i:=i + 2
  • i:=1
  • while i
  • nếu [i] giống với '0' thì s10:=s10 + 1
  • nếu không thì s11:=s11 + 1
  • i:=i + 2
  • s:=s + s00 * s01 * 8
  • s:=s + s10 * s11 * 8
  • s:=s + s00 * s11 * 4
  • s:=s + s10 * s01 * 4
  • n1:=n / 2
  • i:=0
  • while i
  • nếu a [i] không giống với [(i + n1) mod n], thì
    • s:=s - 2
  • i:=i + 1
  • nếu n mod 3 giống 0, thì
    • n1:=n / 3
    • n2:=n1 * 2
    • i:=0
    • while i
    • nếu a [i] không giống với [(i + n1) mod n], thì
      • s:=s - 2
    • nếu a [i] không giống với [(i + n2) mod n], thì
      • s:=s - 2
    • i:=i + 1
  • trả về s / 2
  • Từ phương pháp chính, hãy thực hiện như sau -
  • n:=kích thước của đa giác
  • no:=all (n) - non (polygon, n) / 2
  • trả lại không

    • Ví dụ

    Hãy cùng chúng tôi xem cách triển khai sau để hiểu rõ hơn - 

    def all(n):
   if n % 2 == 1:
      no = n*(n-1)/2
   else:
      no = n*(n/2-1)
   if n % 3 == 0:
      no -= n/3*2
   return no

def non(a,n):
   if n % 2 == 1:
      s0 = s1 = 0
      i = 0
      while i < n:
         if a[i] == '0':
            s0 += 1
         else:
            s1 += 1
         i += 1
      s = s0*s1*6
      if n % 3 == 0:
         n1 = n/3
         n2 = n1*2
         i = 0
         while i<n:
            if a[i] != a[int((i+n1)%n)]:
               s -= 2
            if a[i] != a[int((i+n2)%n)]:
               s -= 2
            i += 1
   else:
      s00 = s01 = s10 = s11 = s = 0
      i = 0
      while i <n:
         if a[i] == '0':
            s00 += 1
         else:
            s01 += 1
         i += 2
      i = 1
      while i < n:
         if a[i] == '0':
            s10 += 1
         else:
            s11 += 1
         i += 2
      s += s00 * s01 * 8
      s += s10 * s11 * 8
      s += s00 * s11 * 4
      s += s10 * s01 * 4
      n1 = n/2
      i = 0
      while i < n:
         if a[i] != a[int((i + n1)%n)]:
            s -= 2
         i += 1
      if n % 3 == 0:
         n1 = n/3
         n2 = n1*2
         i = 0
         while i < n:
            if a[i] != a[int((i+n1)%n)]:
               s -= 2
            if a[i] != a[int((i+n2)%n)]:
               s -= 2
            i += 1
   return s/2

def solve(polygon):
   n = len(polygon)
   no = all(n) - non(polygon,n)/2
   return int(no)

polygon = "111010"
print(solve(polygon))

    Đầu vào 

    1, 1000

    Đầu ra 

    2