Giả sử chúng ta có n nút khác nhau. Tất cả đều khác biệt. Chúng ta phải tìm xem có bao nhiêu cách sắp xếp chúng để tạo thành cây tìm kiếm nhị phân. Như chúng ta đã biết đối với cây tìm kiếm nhị phân, cây con bên trái luôn giữ giá trị nhỏ hơn và cây con bên phải giữ giá trị lớn hơn.
Để giải quyết vấn đề này, chúng ta sẽ tìm số Catalan. Số Catalan C (n) đại diện cho cây tìm kiếm nhị phân với n khóa khác nhau. Công thức giống như
$$ C (n) =\ frac {(2n)!} {(N + 1)! \ Times n!} $$
Vì vậy, nếu đầu vào là n =3, thì đầu ra sẽ là 5 vì
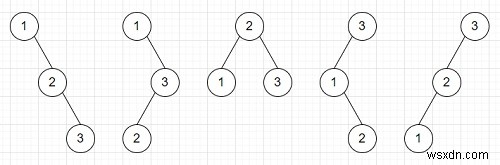
Để giải quyết vấn đề này, chúng tôi sẽ làm theo các bước sau -
- Định nghĩa một hàm ncr (). Điều này sẽ mất n, r
- res:=1
- nếu r> n - r, thì
- r:=n - r
- đối với tôi trong phạm vi từ 0 đến r - 1, thực hiện
- res:=res * (n - i)
- res:=tầng của (res / (i + 1))
- trả lại res
- Từ phương pháp chính, hãy thực hiện như sau
- c:=ncr (2 * n, n)
- tầng trả lại của c / (n + 1)
Ví dụ
Hãy cùng chúng tôi xem cách triển khai sau để hiểu rõ hơn -
from math import factorial def ncr(n, r): res = 1 if r > n - r: r = n - r for i in range(r): res *= (n - i) res //= (i + 1) return res def solve(n): c = ncr(2 * n, n) return c // (n + 1) n = 3 print(solve(n))
Đầu vào
3
Đầu ra
5
