Tích của N phân số đã cho ở dạng rút gọn trong C

Với tử số và mẫu số của N phân số, nhiệm vụ là tìm tích của N phân số và sản lượng phải ở dạng rút gọn.

Giống như trong hình bên dưới, chúng ta có hai phân số "4/5" và "3/4", chúng ta đã tìm thấy tích của hai phái đó trong đó tử số của thứ nhất nhân với tử số thứ hai và mẫu số của thứ nhất là nhân mẫu số của thứ hai. Bây giờ kết quả cuối cùng là “12/20” có thể được giảm xuống vì vậy đầu ra sẽ là “3/5”, tương tự như vậy, chúng tôi phải phát triển một chương trình để giải quyết vấn đề đã cho.

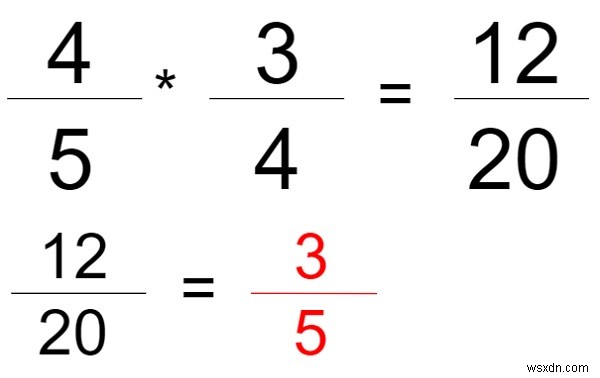
Đầu vào

fraction f[3] = {{1,2},
{2,1},
{5,6}}

Đầu ra

5/6

Giải thích - 1/2 * 2/1 * 5/6 =10/12 nên chúng ta có thể giảm nó thành 5/6.

Đầu vào

fraction f[2] = {{2, 3},
{1,4}}

Đầu ra

1/6

Giải thích - 2/3 * 1/4 =2/12 có thể giảm xuống còn 1/6

Phương pháp được sử dụng dưới đây như sau để giải quyết vấn đề

Để giải quyết vấn đề trên, chúng ta có thể tích tất cả các mẫu số và tử số, lưu trữ kết quả trong một biến khác prod_den và prod_num sẽ là mẫu số cuối cùng và tử số cuối cùng tương ứng, bây giờ chúng ta phải tìm dạng rút gọn, vì vậy chúng ta phải tìm GCD (ước số chung lớn nhất) của prod_num và prod_den và chia prod_num và prod_den với GCD tương ứng của chúng.

Thuật toán

Start
Declare a struct fraction with following elements
   1. num, 2. den
In function int GCD(int a, int b)
   Step 1→ If a == 0 then,
      Return b
   Step 2→ Return GCD(b % a, a)
In function int product(int n, fraction f[])
   Step 1→ Initialize prod_num = 1 prod_den = 1
   Step 2→ Loop For i = 0; i < n; i++
      prod_num = prod_num * f[i].num
      prod_den = prod_den * f[i].den
   Step 3→ Declare and initialize gcd = GCD(prod_num, prod_den)
   Step 4→ prod_num = prod_num / gcd
   Step 5→ prod_den = prod_den / gcd
   Step 6→ Print prod_num, prod_den
In Function int main()
   Step 1→ Declare struct fraction f[3] = {
      {1,2},
      {2,1},
      {5,6}}
   Step 2→ Declare and initialization n as sizeof(f)/sizeof(f[0])
   Step 3→ product(n, f)
Stop

Ví dụ

#include <stdio.h>
struct fraction{
   int num;
   int den;
};
// Function to return gcd of a and b
int GCD(int a, int b){
   if (a == 0)
      return b;
   return GCD(b % a, a);
}
//fucntion to print the result
int product(int n, fraction f[]){
   int prod_num = 1, prod_den = 1;
   // finding the product of all N
   // numerators and denominators.
   for (int i = 0; i < n; i++) {
      prod_num *= f[i].num;
      prod_den *= f[i].den;
   }
   // Finding GCD of new numerator and
   // denominator
   int gcd = GCD(prod_num, prod_den);
   // finding reduced form
   prod_num /= gcd;
   prod_den /= gcd;
   printf("%d/%d\n", prod_num, prod_den);
   return 0;
}
int main(){
   struct fraction f[3] = {
      {1,2},
      {2,1},
      {5,6}};
   int n = sizeof(f)/sizeof(f[0]);
   product(n, f);
   return 0;
}

Đầu ra

Nếu chạy đoạn mã trên, nó sẽ tạo ra kết quả sau -

5/6