Trong phần này, chúng tôi giải thích cách (2,4) -trees có thể hỗ trợ tìm kiếm ngón tay hiệu quả bằng cách giới thiệu các liên kết cấp. Các ý tưởng được giải thích trong phần này cũng áp dụng cho loại cây cân bằng chiều cao tổng quát hơn được ký hiệu (a, b) -trees, cho b ≥ 2a.
A (2,4) -tree được định nghĩa là cây tìm kiếm cân bằng độ cao trong đó tất cả các lá có cùng độ sâu và tất cả các nút bên trong có bậc hai, ba hoặc bốn. Các phần tử được lưu trữ tại các lá và các nút bên trong chỉ lưu trữ các khóa tìm kiếm để hướng dẫn tìm kiếm. Vì mỗi nút bên trong có bậc ít nhất là hai, theo đó a (2,4) -bóng có độ cao O (log n) và hỗ trợ tìm kiếm trong thời gian O (log n). Một thuộc tính quan trọng của (2,4) -trees là các lần chèn và xóa do một ngón tay cung cấp sẽ được phân bổ theo thời gian O (1) (thuộc tính này không được chia sẻ bởi (2, 3) -trees, trong đó tồn tại các chuỗi của m lần chèn và xóa yêu cầu Θ (m log m) thời gian). Hơn nữa, một (2,4) - cây có m lá có thể được tách thành hai cây có kích thước m1 và m2 theo thời gian O (log min (m1, m2)) được khấu hao. Tương tự, hai (2,4)-ba kích thước m1 và m2 có thể được kết hợp (ghép nối) theo thời gian O (log min (m1, m2)) được phân bổ.
Để hỗ trợ tìm kiếm bằng ngón tay, (2,4) -trees được tăng cường với các liên kết cấp, sao cho tất cả các nút có độ sâu bằng nhau được liên kết với nhau trong một danh sách được liên kết kép. Hình sau hiển thị một (2,4) -bộ được tăng cường với các liên kết cấp. Hãy nhớ tất cả các cạnh đại diện cho các liên kết được điều hướng. Các liên kết cấp bổ sung dễ bảo quản trong quá trình chèn, xóa, tách và nối (2,4) -trees.
Để thực hiện tìm kiếm theo ngón tay từ X đến Y, trước tiên, chúng tôi kiểm tra xem Y nằm ở bên trái hay bên phải của X. Giả sử rằng Y ở bên phải của X. các nút V trên đường đi và các nút lân cận bên phải của chúng cho đến khi nó được thiết lập rằng Y được chứa trong cây con bắt nguồn từ V hoặc lân cận bên phải của V. Sau đó, tìm kiếm hướng lên được kết thúc và nhiều nhất hai tìm kiếm hướng xuống đối với y được bắt đầu lần lượt ở V và / hoặc hàng xóm bên phải của V. Trong Hình 1, các con trỏ theo sau trong quá trình tìm kiếm ngón tay từ j đến t được biểu thị bằng các đường dày.
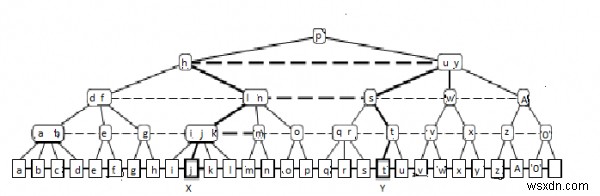
Thời gian tìm kiếm O (log d) xuất phát từ quan sát rằng nếu chúng ta tiến hành tìm kiếm lên trên đến nút cha của nút V thì nút Y ở bên phải cây con ngoài cùng bên trái của nút lân cận bên phải của V, tức là d ít nhất là hàm mũ trong chiều cao đạt được cho đến nay.
Trong Hình 1, chúng ta tiến từ nút bên trong có nhãn “l n” đến nút có nhãn “h” vì từ “s”, chúng ta biết rằng Y ở bên phải cây con được sắp xếp tại nút “q r”.
Cấu trúc cho các cấp được liên kết (2,4) -trees tổng quát trực tiếp thành cấp độ được liên kết (a, b) -trees có thể được thực hiện trong bộ nhớ ngoài. Bằng cách chọn a =2b và b sao cho nút bên trong phù hợp với một khối trong bộ nhớ ngoài, chúng tôi đạt được cây tìm kiếm ngón tay bộ nhớ ngoài hỗ trợ chèn và xóa trong chuyển bộ nhớ O (1) và tìm kiếm ngón tay với chuyển bộ nhớ O (logb n) .
