Cây tìm kiếm nhị phân tối ưu

Một tập hợp các số nguyên được đưa ra theo thứ tự đã sắp xếp và một mảng khác tần suất đếm tần suất. Nhiệm vụ của chúng tôi là tạo một cây tìm kiếm nhị phân với những dữ liệu đó để tìm ra chi phí tối thiểu cho tất cả các tìm kiếm.

Một mảng phụ trợ cost [n, n] được tạo ra để giải và lưu trữ lời giải của các bài toán con. Ma trận chi phí sẽ giữ dữ liệu để giải quyết vấn đề theo cách từ dưới lên.

Đầu vào và Đầu ra

Input:
The key values as node and the frequency.
Keys = {10, 12, 20}
Frequency = {34, 8, 50}
Output:
The minimum cost is 142.
These are possible BST from the given values.
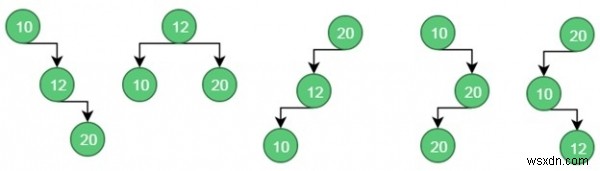For case 1, the cost is: (34*1) + (8*2) + (50*3) = 200
For case 2, the cost is: (8*1) + (34*2) + (50*2) = 176.
Similarly for case 5, the cost is: (50*1) + (34 * 2) + (8 * 3) = 142 (Minimum)

Thuật toán

optCostBst(keys, freq, n)

Đầu vào: Các phím cần chèn trong BST, tần suất cho mỗi khóa, số lượng khóa.

Đầu ra: Chi phí tối thiểu để tạo nên BST tối ưu.

Begin
   define cost matrix of size n x n
   for i in range 0 to n-1, do
      cost[i, i] := freq[i]
   done

   for length in range 2 to n, do
      for i in range 0 to (n-length+1), do
         j := i + length – 1
         cost[i, j] := ∞
         for r in range i to j, done
            if r > i, then
               c := cost[i, r-1]
            else
               c := 0
            if r < j, then
               c := c + cost[r+1, j]
            c := c + sum of frequency from i to j
            if c < cost[i, j], then
               cost[i, j] := c
         done
      done
   done
   return cost[0, n-1]
End

Ví dụ

#include <iostream>
using namespace std;

int sum(int freq[], int low, int high) {    //sum of frequency from low to high range
   int sum = 0;
   for (int k = low; k <=high; k++)
      sum += freq[k];
   return sum;
}

int minCostBST(int keys[], int freq[], int n) {
   int cost[n][n];

   for (int i = 0; i < n; i++)    //when only one key, move along diagonal elements
      cost[i][i] = freq[i];

   for (int length=2; length<=n; length++) {
      for (int i=0; i<=n-length+1; i++) {    //from 0th row to n-length+1 row as i
         int j = i+length-1;
         cost[i][j] = INT_MAX;    //initially store to infinity

         for (int r=i; r<=j; r++) {
            //find cost when r is root of subtree
            int c = ((r > i)?cost[i][r-1]:0)+((r < j)?cost[r+1][j]:0)+sum(freq, i, j);
            if (c < cost[i][j])
               cost[i][j] = c;
         }
      }
   }
   return cost[0][n-1];
}

int main() {
   int keys[] = {10, 12, 20};
   int freq[] = {34, 8, 50};
   int n = 3;
   cout << "Cost of Optimal BST is: "<< minCostBST(keys, freq, n);
}

Đầu ra

Cost of Optimal BST is: 142