Sắp xếp theo cấu trúc liên kết

Việc sắp xếp tôpô cho một đồ thị xoay chiều có hướng là thứ tự tuyến tính của các đỉnh. Đối với mọi cạnh U-V của đồ thị có hướng, đỉnh u sẽ đến trước đỉnh v theo thứ tự.

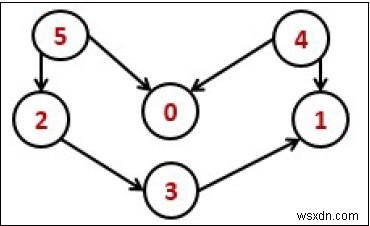
Như chúng ta biết rằng đỉnh nguồn sẽ đến sau đỉnh đích, vì vậy chúng ta cần sử dụng một ngăn xếp để lưu trữ các phần tử trước đó. Sau khi hoàn thành tất cả các nút, chúng tôi chỉ cần hiển thị chúng từ ngăn xếp.

Đầu vào và Đầu ra

Input:
0 0 0 0 0 0
0 0 0 0 0 0
0 0 0 1 0 0
0 1 0 0 0 0
1 1 0 0 0 0
1 0 1 0 0 0

Output:
Nodes after topological sorted order: 5 4 2 3 1 0

Thuật toán

topoSort (u, đã truy cập, ngăn xếp)

Đầu vào - Đỉnh bắt đầu u, Một mảng để theo dõi xem nút nào được truy cập hay không. Một ngăn xếp để lưu trữ các nút.
Đầu ra - Sắp xếp các đỉnh theo trình tự tôpô trong ngăn xếp.

Begin
   mark u as visited
   for all vertices v which is adjacent with u, do
      if v is not visited, then
         topoSort(c, visited, stack)
   done

   push u into a stack
End

performanceTopologicalSorting (Graph)

Đầu vào - Đồ thị mạch hở có hướng đã cho.
Đầu ra - Trình tự các nút.

Begin
   initially mark all nodes as unvisited
   for all nodes v of the graph, do
      if v is not visited, then
         topoSort(i, visited, stack)
   done
   pop and print all elements from the stack
End.

Ví dụ

#include<iostream>
#include<stack>
#define NODE 6
using namespace std;

int graph[NODE][NODE] = {
   {0, 0, 0, 0, 0, 0},
   {0, 0, 0, 0, 0, 0},
   {0, 0, 0, 1, 0, 0},
   {0, 1, 0, 0, 0, 0},
   {1, 1, 0, 0, 0, 0},
   {1, 0, 1, 0, 0, 0}
};

void topoSort(int u, bool visited[], stack<int>&stk) {
   visited[u] = true;                //set as the node v is visited

   for(int v = 0; v<NODE; v++) {
      if(graph[u][v]) {             //for allvertices v adjacent to u
         if(!visited[v])
            topoSort(v, visited, stk);
      }
   }
   stk.push(u);     //push starting vertex into the stack
}

void performTopologicalSort() {
   stack<int> stk;
   bool vis[NODE];

   for(int i = 0; i<NODE; i++)
      vis[i] = false;     //initially all nodes are unvisited

   for(int i = 0; i<NODE; i++)
      if(!vis[i])     //when node is not visited
         topoSort(i, vis, stk);

   while(!stk.empty()) {
      cout << stk.top() << " ";
      stk.pop();
   }
}

main() {
   cout << "Nodes after topological sorted order: ";
   performTopologicalSort();
}

Đầu ra

Nodes after topological sorted order: 5 4 2 3 1 0