Ở đây chúng ta sẽ xem cách lấy hai chữ số cuối cùng. Chữ số hàng đơn vị và chữ số hàng chục của tổng N thừa số. Vì vậy, nếu N =4, nó sẽ là 1! + 2! + 3! + 4! =33. vậy vị trí đơn vị là 3 và vị trí mười là 3. Kết quả sẽ là 33.
Nếu chúng ta thấy rõ điều này, thì do thừa số của N> 5, hàng đơn vị là 0, vì vậy sau 5, nó sẽ không góp phần thay đổi hàng đơn vị. Và sau N> 10, mười vị trí sẽ còn lại 0. Đối với N =10 trở lên, nó sẽ là 00. Chúng ta có thể lập biểu đồ cho N =1 đến 10 của các số giai thừa.
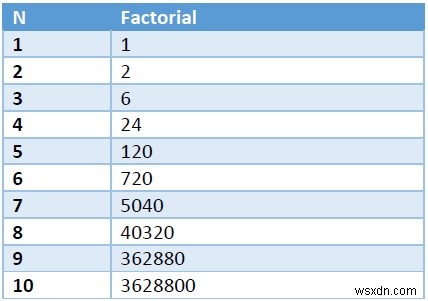
Chúng tôi có thể giải quyết vấn đề này bằng cách sử dụng các bước sau -
- Nếu giá trị của n nhỏ hơn 10, thì (1! + 2! +… + n!) mod 10
- ngược lại khi giá trị của n lớn hơn hoặc bằng 10 thì (1! + 2! +… + 10!) mod 10 =13
Ví dụ
#include<iostream>
#include<cmath>
using namespace std;
int getTenAndUnitPlace(long long N) {
if (N <= 10) {
long long ans = 0, factorial = 1;
for (int i = 1; i <= N; i++) {
factorial = factorial * i;
ans += factorial;
}
return ans % 100;
}
return 13;
}
int main() {
for(long long i = 1; i<15; i++){
cout << "Ten and Unit place value of sum of factorials when N = "<<i<<" is: " <<getTenAndUnitPlace(i) << endl;
}
} Đầu ra
Ten and Unit place value of sum of factorials when N = 1 is: 1 Ten and Unit place value of sum of factorials when N = 2 is: 3 Ten and Unit place value of sum of factorials when N = 3 is: 9 Ten and Unit place value of sum of factorials when N = 4 is: 33 Ten and Unit place value of sum of factorials when N = 5 is: 53 Ten and Unit place value of sum of factorials when N = 6 is: 73 Ten and Unit place value of sum of factorials when N = 7 is: 13 Ten and Unit place value of sum of factorials when N = 8 is: 33 Ten and Unit place value of sum of factorials when N = 9 is: 13 Ten and Unit place value of sum of factorials when N = 10 is: 13 Ten and Unit place value of sum of factorials when N = 11 is: 13 Ten and Unit place value of sum of factorials when N = 12 is: 13 Ten and Unit place value of sum of factorials when N = 13 is: 13 Ten and Unit place value of sum of factorials when N = 14 is: 13
