Cho điểm A, B tương ứng với đường thẳng AB và điểm P, Q tương ứng với đường thẳng PQ; nhiệm vụ là tìm giao điểm giữa hai đường này.
Lưu ý - Các điểm được cho trong mặt phẳng 2D trên các tọa độ X và Y.
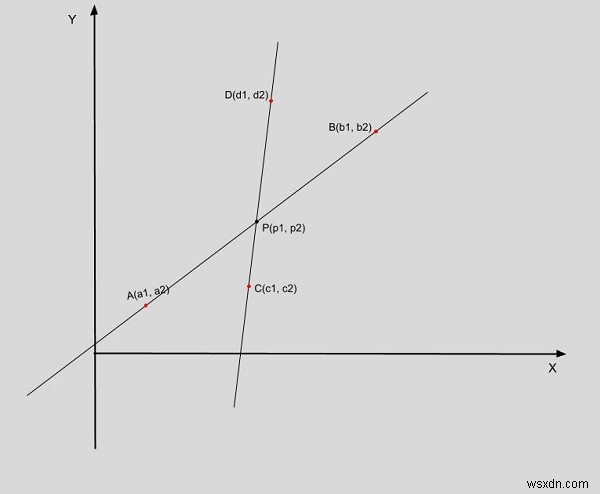
Ở đây A (a1, a2), B (b1, b2) và C (c1, c2), D (d1, d2) là tọa độ tạo thành hai đường thẳng phân biệt và P (p1, p2) là giao điểm. (chỉ để giải thích sơ đồ về điểm giao nhau)
Cách tìm giao điểm -
Hãy coi con số trên là -
Ví dụ
So using the (a1, a2), (b1, b2), (c1, c2), (d1, d2) We will calculate : A1 = b2 - a2 B1 = a1 - b1 C1 = (A1 * a1) + (B1 * a1) A2 = d2 - c2 B2 = c1 - d1 C2 = (A2 * c1) + (B2 * c2) Let the given lines be: 1. A1x + B1y = C1 2. A2x + B2y = C2 Now, to find the point of intersection, we have to solve these 2 equations. We will multiply 1 by B1 and 2 by B2, so we will get: A1B2x +B1B2y = C1B2 A1B1x +B2B1y = C1B1 Subtracting these we get, (A1B2 - A2B1)x = C1B2-C2B1
Điều này cho chúng ta giá trị của x và tương tự, chúng ta sẽ nhận được giá trị của y sẽ là giao điểm của p1 là x và p2 là y.
Lưu ý - công thức trên sẽ cho biết giao điểm của hai đường thẳng, nhưng nếu các đoạn được cho thay vì các đoạn thẳng thì chúng ta phải kiểm tra lại điểm đó nên kết quả tính toán phải nằm trên đoạn thẳng.
- tối thiểu (x1, x2) <=x <=max (x1, x2)
- tối thiểu (y1, y2) <=y <=max (y1, y2)
Phương pháp tiếp cận mà chúng tôi đang sử dụng để giải quyết vấn đề trên -
- Lấy các giá trị đầu vào.
- Tìm định thức là a1 * b2 - a2 * b1
- Kiểm tra nếu định thức =0 thì các đường thẳng song song
- Nếu định thức không bằng 0 thì x =(c1 * b2 - c2 * b1) và y =(a1 * c2 - a2 * c1)
- Trả lại và in kết quả.
Thuật toán
Start Step 1-> Declare function to print the x and y coordinates void display(mk_pair par) Print par.first and par.second Step 2-> declare function to calculate the intersection point mk_pair intersection(mk_pair A, mk_pair B, mk_pair C, mk_pair D) Declare double a = B.second - A.second Declare double b = A.first - B.first Declare double c = a*(A.first) + b*(A.second) Declare double a1 = D.second - C.second Declare double b1 = C.first - D.first Declare double c1 = a1*(C.first)+ b1*(C.second) Declare double det = a*b1 - a1*b IF (det = 0) return make_pair(FLT_MAX, FLT_MAX) End Else Declare double x = (b1*c - b*c1)/det Declare double y = (a*c1 - a1*c)/det return make_pair(x, y) End Step 3-> In main() Declare and call function for points as mk_pair q = make_pair(2, 1) IF (inter.first = FLT_MAX AND inter.second = FLT_MAX) Print “given lines are parallel“ End Else Call display(inter) End Stop
Ví dụ
#include <bits/stdc++.h>
using namespace std;
#define mk_pair pair<double, double>
//display the x and y coordinates
void display(mk_pair par) {
cout << "(" << par.first << ", " << par.second << ")" << endl;
}
mk_pair intersection(mk_pair A, mk_pair B, mk_pair C, mk_pair D) {
// Line AB represented as a1x + b1y = c1
double a = B.second - A.second;
double b = A.first - B.first;
double c = a*(A.first) + b*(A.second);
// Line CD represented as a2x + b2y = c2
double a1 = D.second - C.second;
double b1 = C.first - D.first;
double c1 = a1*(C.first)+ b1*(C.second);
double det = a*b1 - a1*b;
if (det == 0) {
return make_pair(FLT_MAX, FLT_MAX);
} else {
double x = (b1*c - b*c1)/det;
double y = (a*c1 - a1*c)/det;
return make_pair(x, y);
}
}
int main() {
mk_pair q = make_pair(2, 1);
mk_pair r = make_pair(2, 7);
mk_pair s = make_pair(4, 4);
mk_pair t = make_pair(6, 4);
mk_pair inter = intersection(q, r, s, t);
if (inter.first == FLT_MAX && inter.second==FLT_MAX) {
cout << "The given lines AB and CD are parallel.\n";
} else {
cout << "The intersection of the given lines AB and CD is: ";
display(inter);
}
return 0;
} Đầu ra
The intersection of the given lines AB and CD is: (2, 4)
