Cho hàm f (x) với các số a và b trong đó f (a) * f (b)> 0 và hàm f (x) nên nằm giữa a và b tức là f (x) =[a, b ]. Nhiệm vụ là tìm giá trị của căn nằm giữa khoảng a và b trong hàm f (x) bằng phương pháp phân giác.
Phương pháp chia đôi là gì?
Phương pháp phân tách được sử dụng để tìm giá trị của một gốc trong hàm f (x) trong các giới hạn cho trước được xác định bởi ‘a’ và ‘b’. Gốc của hàm có thể được xác định là giá trị a sao cho f (a) =0.
Ví dụ
Quadratic equation F(x) = - 8 This equation is equals to 0 when the value of x will be 2 i.e. - 8 = 0 So, root of this quadratic function F(x) will be 2.
Bây giờ, Nếu một hàm f (x) liên tục trong khoảng [a..b] đã cho và đồng thời, dấu của f (a) ≠ dấu của f (b) thì sẽ có giá trị m thuộc khoảng a và b sao cho f (m) =0
Giá trị m [a..b] Sao cho f (m) =0
I E. m là giá trị của gốc có thể là nhiều
Cho dưới đây là hình biểu diễn các khoảng f (a) và f (b). Để tìm gốc giữa các khoảng này, giới hạn được chia thành các phần và được lưu trữ trong biến m i.e.
m =(a + b) / 2
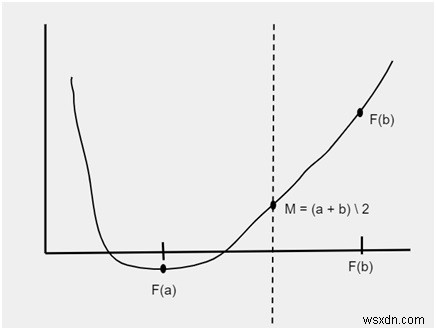
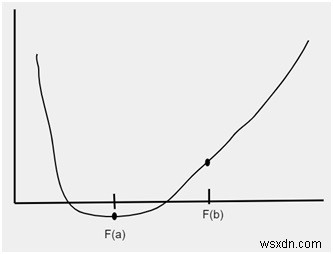
Sau khi phân chia các giới hạn, khoảng thời gian mới sẽ được tạo ra như trong hình bên dưới
Ví dụ
Input-: x^3 - x^2 + 2 ; a =-500 and b = 100 Output-: The value of root is : -0.991821 Input-: x^3 - x^2 + 2 ; a =-200 and b = 300 Output-: The value of root is : -1.0025
Phương pháp tiếp cận mà chúng tôi đang sử dụng trong chương trình dưới đây như sau -
- Nhập phương trình và giá trị của các khoảng a và b
- Chia các khoảng dưới dạng:m =(a + b) / 2
- In m là gốc
- Nếu f (m) ≠ 0
- Kiểm tra xem f (a) * f (m) <0
- Khi đó, gốc sẽ nằm giữa a và m
- Kiểm tra xem f (b) * f (m) <0
- Khi đó gốc sẽ nằm giữa b và m
Thuật toán
Start Step 1-> In function double solution(double x) Return x*x*x - x*x + 2 Step 2-> In function bisection(double a, double b) If solution(a) * solution(b) >= 0 then, Print "You have not assumed right a and b " Return End If Set c = a Loop While (b-a) >= EP Set c = (a+b)/2 If solution(c) == 0.0 Break End If Else if solution(c)*solution(a) < 0 Set b = c End Else If Else Set a = c End Else End Print "The value of root” Step 3-> In function int main() Declare and Initialize inputs a =-500, b = 100 Call function bisection(a, b) Stop
Ví dụ
#include <iostream>
using namespace std;
#define EP 0.01
// An example function whose solution is determined using
// Bisection Method. The function is x^3 - x^2 + 2
double solution(double x) {
return x*x*x - x*x + 2;
}
// Prints root of solution(x) with error in EPSILON
void bisection(double a, double b) {
if (solution(a) * solution(b) >= 0) {
cout << "You have not assumed right a and b\n";
return;
}
double c = a;
while ((b-a) >= EP) {
// Find middle point
c = (a+b)/2;
// Check if middle point is root
if (solution(c) == 0.0)
break;
// Decide the side to repeat the steps
else if (solution(c)*solution(a) < 0)
b = c;
else
a = c;
}
cout << "The value of root is : " << c;
}
// main function
int main() {
double a =-500, b = 100;
bisection(a, b);
return 0;
} Đầu ra
The value of root is : -0.991821
