Giả sử một tên trộm đã tìm thấy cho mình một địa điểm mới để thực hiện hành vi trộm cắp một lần nữa. Chỉ có một lối vào khu vực này, lối vào được gọi là "gốc". Ngoài gốc đa, mỗi nhà có một và chỉ một nhà cha. Sau một vòng tham quan, tên trộm thông minh cảm thấy rằng "tất cả các ngôi nhà ở nơi này đều tạo thành một cây nhị phân". Và nó sẽ tự động liên lạc với cảnh sát nếu hai ngôi nhà liên kết trực tiếp bị đột nhập vào cùng một đêm. Chúng ta phải tìm ra số tiền tối đa mà tên trộm có thể cướp được trong đêm nay mà không cần báo cho cảnh sát. Vì vậy, nếu cây như -
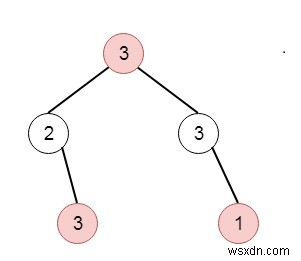
Khi đó đầu ra sẽ là 7.
Để giải quyết vấn đề này, chúng tôi sẽ làm theo các bước sau -
-
Xác định một phương thức có tên là giải quyết (), phương thức này sẽ sử dụng nút
-
nếu nút là null, thì trả về một cặp (-infinity, 0)
-
leftVal:=left of node, rightVal:=right of node
-
phần tử đầu tiên của leftVal:=tối đa phần tử đầu tiên của leftVal và 0
-
phần tử thứ hai của leftVal:=tối đa phần tử thứ hai của leftVal và 0
-
phần tử đầu tiên của rightVal:=tối đa phần tử đầu tiên của rightVal và 0
-
phần tử thứ hai của rightVal:=tối đa phần tử thứ hai của rightVal và 0
-
currVal:=max của giá trị của nút và 0
-
cantBeAdded:=currVal + giá trị thứ hai của leftVal + giá trị thứ hai của rightVal
-
canBeAdded:=max of (giá trị đầu tiên của leftVal + giá trị đầu tiên của rightVal) và tối đa (giá trị thứ hai của leftVal, giá trị thứ hai của rightVal, giá trị thứ hai của leftVal + giá trị thứ hai của rightVal, giá trị thứ hai của leftVal + giá trị thứ nhất của rightVal, giá trị thứ hai của rightVal + giá trị đầu tiên của leftVal)
-
Trả lại một cặp (cantBeAdded, canBeAdded)
-
Trong phương thức main, hãy tạo a:=giải quyết (root), sau đó trả về giá trị lớn nhất của giá trị đầu tiên của a và giá trị thứ hai của a.
Ví dụ (C ++)
Hãy cùng chúng tôi xem cách triển khai sau đây để hiểu rõ hơn -
#include <bits/stdc++.h>
using namespace std;
class TreeNode{
public:
int val;
TreeNode *left, *right;
TreeNode(int data){
val = data;
left = right = NULL;
}
};
void insert(TreeNode **root, int val){
queue<TreeNode*> q;
q.push(*root);
while(q.size()){
TreeNode *temp = q.front();
q.pop();
if(!temp->left){
if(val != NULL)
temp->left = new TreeNode(val);
else
temp->left = new TreeNode(0);
return;
}
else{
q.push(temp->left);
}
if(!temp->right){
if(val != NULL)
temp->right = new TreeNode(val);
else
temp->right = new TreeNode(0);
return;
} else {
q.push(temp->right);
}
}
}
TreeNode *make_tree(vector<int> v){
TreeNode *root = new TreeNode(v[0]);
for(int i = 1; i<v.size(); i++){
insert(&root, v[i]);
}
return root;
}
const int INF = -1e8;
class Solution {
public:
void printData(pair <int,int> t){
cout << t.first << " " << t.second << endl;
}
pair <int,int> solve(TreeNode* node){
if(!node){
return {INF,0};
}
pair <int,int> leftVal = solve(node->left);
pair <int,int> rightVal = solve(node->right);
leftVal.first = max(leftVal.first,0);
leftVal.second = max(leftVal.second,0);
rightVal.second = max(rightVal.second,0);
rightVal.first = max(rightVal.first,0);
int currentVal = max(node->val,0);
int cantBeAdded = currentVal + leftVal.second + rightVal.second;
int canBeAdded =max(leftVal.first + rightVal.first,max({
leftVal.second,rightVal.second,leftVal.second
+ rightVal.second,leftVal.second+rightVal.first,rightVal.second+leftVal.first
}));
return {cantBeAdded,canBeAdded};
}
int rob(TreeNode* root) {
pair <int,int> a = solve(root);
return max(a.first,a.second);
}
};
main(){
Solution ob;
vector<int> v = {3,2,3,NULL,3,NULL,1};
TreeNode *root = make_tree(v);
cout << (ob.rob(root));
} Đầu vào
[3,2,3,null,3,null,1]
Đầu ra
7
