Các cách để đặt các mục ở n ^ 2 vị trí sao cho không có hàng / cột nào chứa nhiều hơn một trong C ++

Trong bài toán này, chúng ta được cho một số nguyên n sao cho có n đường thẳng đứng và n đường thẳng nằm ngang được đặt sao cho có n2 giao điểm giữa các đường thẳng này. Nhiệm vụ của chúng ta là tìm tổng số cách có thể đặt 4 vật phẩm trên các giao lộ này ở

sao cho không có hàng và cột nào chứa nhiều hơn một mục.

Hãy lấy một ví dụ để hiểu vấn đề,

Đầu vào

n=4

Đầu ra

24

Giải thích

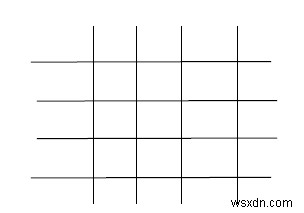
Để giải quyết vấn đề này, chúng ta sẽ phải chọn 4 hàng ngang từ n dòng sẽ có các mục sẽ là nC4. Bây giờ, mỗi hàng ngang có n đường thẳng đứng, do đó, sẽ có n cách để đặt một mục trong hàng ngang được chọn đầu tiên. Sau đó, chúng tôi sẽ chuyển đến dòng ngang được chọn tiếp theo, nơi sẽ có n-1 vị trí có thể. Và nó theo cùng một cách thứ ba có thể được đặt trong n-2 và thứ hai trong n-3 cách. Vì vậy, tổng số wats sẽ là ⁿ C4 * n * (n-1) * (n-2) * (n-3)

Chương trình hiển thị việc triển khai thuật toán,

Ví dụ

#include <iostream>
using namespace std;
long long placeItems(int n) {
   return (1LL * (1LL *
   ((n) * (n - 1) * (n - 2) * (n - 3)) / (4 * 3 * 2 * 1)) *
   ((1LL * (n) * (n - 1) * (n - 2) * (n - 3))));
}
int main() {
   int n = 4;
   cout<<"The number of way is which 4 items can be placed in the intersection of "<<n;
   cout<<" lines vertically and horizotally are "<<placeItems(n);
   return 0;
}

Đầu ra

The number of way is which 4 items can be placed in the intersection of 4 lines vertically and horizotally are 24