Xoay một điểm về một điểm khác trong C ++

Phép quay của điểm X về gốc tọa độ một góc θ theo hướng ngược chiều kim đồng hồ được thực hiện bằng -

X theo θ về nguồn gốc ngược clRotateockwise:X * cực (1,0, θ).

Ở đây, cực của hàm cho số phức được định nghĩa trong tệp tiêu đề và được sử dụng để tìm một số phức bằng cách sử dụng góc pha và độ lớn .polar (mag, angle) trả về một số phức.

Xoay điểm X về điểm Y

Để xoay một điểm về một điểm khác, chúng tôi sẽ sử dụng phép tịnh tiến trong đó chuyển động của tất cả các tọa độ xảy ra theo một hướng cụ thể.

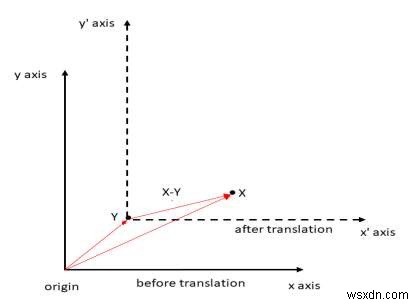
Các bước để xoay X về Y.

• Dịch X thành Y, do đó Y trở thành điểm gốc mới. Điều này có thể được thực hiện bằng cách trừ Y cho tất cả các điểm. X bây giờ trở thành X-Y.

• Xoay (X-Y) về điểm gốc mới bằng công thức trên:(X-Y) * polar (1,0, θ)

• Dịch ngược bằng cách thêm Y vào tất cả các điểm.

Xoay của X về Y là:(X-Y) * polar (1,0, θ) + Y

Dưới đây là mã để chứng minh sự quay của điểm về một điểm khác

Ví dụ

#include <iostream>
#include <complex>
using namespace std;
typedef complex<double> point;
#define x real()
#define y imag()
int main(){
   // Rotate P about Q
   point X(5.0, 3.0);
   point Y(2.0, 4.0);
   // Angle of rotation is 90 degrees
   double theta = 3.14/2;
   point Xnew=(X-Y) * polar(1.0, theta) + Y;
   cout << "rotating X 90 degrees anti-clockwise about Y becomes:";
   cout << "(" << Xnew.x << ", " << Xnew.y << ")" << endl;
   return 0;
}

Đầu ra

rotating X 90 degrees anti-clockwise about Y becomes:(3.00239, 6.9992)