Giả sử có một quả bóng trong một mê cung với không gian trống và những bức tường. Bây giờ quả bóng có thể đi qua những con đường trống bằng cách lăn theo bất kỳ hướng nào như lên, xuống, sang trái hoặc sang phải, nhưng nó sẽ không ngừng lăn cho đến khi va vào tường. Khi quả bóng dừng lại, nó có thể chọn hướng tiếp theo.
Chúng ta phải xuất phát vị trí của bóng, điểm đến và mê cung, chúng ta phải tìm khoảng cách ngắn nhất để quả bóng dừng lại ở đích. Ở đây khoảng cách thực sự được xác định bởi số lượng ô trống, được bao phủ bởi quả bóng (Không bao gồm vị trí xuất phát, bao gồm cả vị trí xuất phát). Nếu không thể dừng bóng ở đích, hãy trả về -1.
Mê cung được thể hiện bằng một mảng 2D. Ở đây 1 biểu thị bức tường và 0 biểu thị không gian trống. Các đường viền của mê cung đều là những bức tường. Tọa độ điểm xuất phát và điểm đến được biểu thị bằng các chỉ số hàng và cột.
Vì vậy, nếu đầu vào giống như một mê cung được biểu diễn bởi một mảng 2D
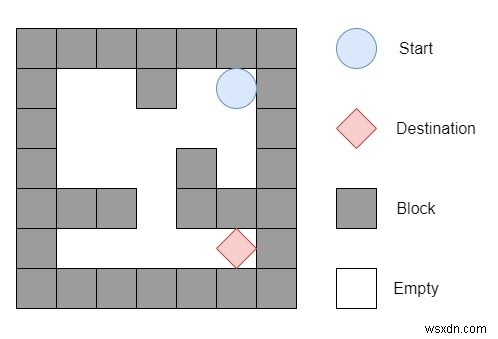
| 0 | 0 | 1 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 | 1 |
| 0 | 0 | 0 | 0 | 0 |
vị trí bắt đầu là (0, 4) vị trí đích là (4, 4), sau đó đầu ra sẽ là 12, Một cách có thể là:từ trái xuống dưới sang trái sang phải xuống phải. (1 + 1 + 3 + 1 + 2 + 2 + 2) =12
Để giải quyết vấn đề này, chúng tôi sẽ làm theo các bước sau -
-
n:=số hàng, m:=số cột
-
ret:=infinity
-
Xác định một phân vùng của mảng 2D theo thứ tự n x m
-
Xác định một hàng đợi q
-
chèn start vào q
-
dist [start [0], start [1]]:=0
-
while (không phải q trống), do -
-
curr:=phần tử đầu tiên của q
-
xóa phần tử khỏi q
-
x:=curr [0], y:=curr [1]
-
nếu x giống với đích [0] và y giống với đích [1], thì -
-
ret:=tối thiểu ret và dist [x, y]
-
-
currDist:=dist [x, y]
-
tempDist:=0
-
i:=x
-
while (i + 1
-
(tăng i lên 1)
-
(tăng tempDist lên 1)
-
-
nếu currDist + tempDist
-
dist [i, y]:=currDist + tempDist
-
chèn {i, y} vào q
-
-
i:=x
-
tempDist:=0
-
trong khi (i - 1> =0 và lưới [i - 1, y] bằng 0), do -
-
(tăng tempDist lên 1)
-
(giảm i đi 1)
-
-
if currDist + tempDist * lt; dist [i, y], sau đó -
-
dist [i, y]:=currDist + tempDist
-
chèn {i, y} vào q
-
-
i:=y
-
tempDist:=0
-
while (i - 1> =0 and grid [x, i - 1] is zero), do -
-
(giảm i đi 1)
-
(tăng tempDist lên 1)
-
-
nếu currDist + tempDist
-
dist [x, i]:=currDist + tempDist
-
chèn {x, i} vào q
-
-
i:=y
-
tempDist:=0
-
trong khi (i + 1
-
(tăng i lên 1)
-
(tăng tempDist lên 1)
-
-
nếu currDist + tempDist
-
dist [x, i]:=currDist + tempDist
-
chèn {x, i} vào q
-
-
-
return (nếu ret giống với inf thì -1, ngược lại là ret)
Ví dụ
Hãy cùng chúng tôi xem cách triển khai sau để hiểu rõ hơn -
#include <bits/stdc++.h>
using namespace std;
class Solution {
public:
int shortestDistance(vector<vector<int<>& grid, vector<int<& start, vector<int<& destination) {
int n = grid.size();
int m = n? grid[0].size() : 0;
int ret = INT_MAX;
vector < vector <int< > dist(n, vector <int<(m, INT_MAX));
queue < vector <int< > q;
q.push(start);
dist[start[0]][start[1]] = 0;
while(!q.empty()){
vector <int< curr = q.front();
q.pop();
int x = curr[0];
int y = curr[1];
if(x == destination[0] && y == destination[1]){
ret = min(ret, dist[x][y]);
}
int currDist = dist[x][y];
int tempDist = 0;
int i = x;
while(i + 1 < n && !grid[i + 1][y]){
i++;
tempDist++;
}
if(currDist + tempDist < dist[i][y]){
dist[i][y] = currDist + tempDist;
q.push({i, y});
}
i = x;
tempDist = 0;
while(i - 1 >= 0 && !grid[i - 1][y]){
tempDist++;
i--;
}
if(currDist + tempDist < dist[i][y]){
dist[i][y] = currDist + tempDist;
q.push({i, y});
}
i = y;
tempDist = 0;
while(i - 1 >= 0 && !grid[x][i - 1]){
i--;
tempDist++;
}
if(currDist + tempDist < dist[x][i]){
dist[x][i] = currDist + tempDist;
q.push({x, i});
}
i = y;
tempDist = 0;
while(i + 1 < m && !grid[x][i + 1]){
i++;
tempDist++;
}
if(currDist + tempDist < dist[x][i]){
dist[x][i] = currDist + tempDist;
q.push({x, i});
}
}
return ret == INT_MAX ? - 1 : ret;
};
main(){
Solution ob;
vector<vector<int<> v = {{0,0,1,0,0},{0,0,0,0,0},{0,0,0,1,0},{1,1,0,1,1},{0,0,0,0,0}};
vector<int< v1 = {0,4}, v2 = {4,4};
cout << (ob.shortestDistance(v, v1, v2));
} Đầu vào
{{0,0,1,0,0},{0,0,0,0,0},{0,0,0,1,0},{1,1,0,1,1},{0,0,0,0,0}}, {0,4},{4,4} Đầu ra
12
