Chúng tôi được cung cấp một ngôn ngữ “L” và nhiệm vụ là xây dựng một dữ liệu tự động kéo xuống cho ngôn ngữ đã cho, giải thích rằng các lần xuất hiện của 0 sẽ là phép cộng các lần xuất hiện của 1 và 2 và ngoài ra, sự xuất hiện của 1 và 2 sẽ là mức tối thiểu cũng có thể làm cho chuỗi NULL và nó phải được tự động chấp nhận.
Dữ liệu tự động kéo xuống là gì?
Tự động dữ liệu đẩy xuống hoặc tự động hóa đẩy xuống hoặc PDA là một kỹ thuật để triển khai ngữ pháp không có văn bản theo cách tương tự mà chúng tôi thiết kế Tự động hóa hữu hạn xác định hoặc DFA cho một ngữ pháp thông thường. DFA có thể hoạt động trên dữ liệu hữu hạn, nhưng PDA có thể hoạt động trên dữ liệu vô hạn. Chúng ta có thể hiểu dữ liệu tự động kéo xuống là sự kết hợp của “máy tiểu bang hữu hạn” và “ngăn xếp”.
Một ô tô tự động đẩy xuống có ba thành phần -
-
một băng đầu vào,
-
một đơn vị điều khiển và
-
ngăn xếp có kích thước vô hạn.
Một PDA có thể được mô tả một cách chính thức là một bộ 7 (Q, Ʃ, S, δ, q0, I, F) -
-
Q là số trạng thái hữu hạn
-
Ʃ là bảng chữ cái đầu vào
-
S là ký hiệu ngăn xếp
-
δ là hàm chuyển tiếp:Q × (Ʃ υ {ε}) × S × Q × S *
-
q0 là trạng thái ban đầu (q0 ε Q)
-
I là ký hiệu đầu ngăn xếp ban đầu (I ε S)
-
F là tập hợp các trạng thái chấp nhận (F ε Q)
Hãy xây dựng một Dữ liệu tự động kéo xuống cho ngôn ngữ nhất định -
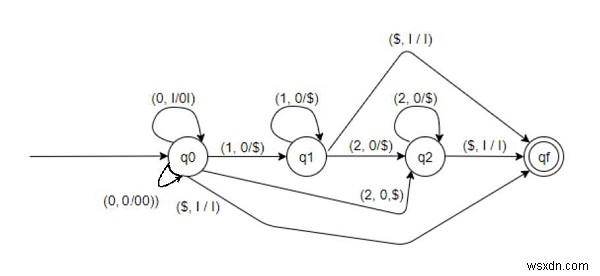
Các chuỗi được PDA này chấp nhận có dạng -
-
1. 0 n 2 n :02, 0022, 000222, v.v. Số 0 bằng không. trong 2 giây. Khi m bằng 0, chúng ta sẽ không có số 1 nào. Tiếp tục đẩy các số 0 và ngay sau khi gặp 2 đầu tiên sau đó bật các số 0. Nếu chúng ta đến cuối chuỗi và không còn số 0 thì chuỗi đó được chấp nhận.
-
0 m 1 m :01, 0011, 000111, v.v. Số 0 bằng không. trong 1 giây. Khi n bằng 0, chúng ta sẽ không có số 2 nào. Tiếp tục đẩy các số 0 và ngay khi gặp số 1 đầu tiên sau đó bật các số 0. Nếu chúng ta đến cuối chuỗi và không còn số 0 thì chuỗi đó được chấp nhận.
-
0 n + m 1 m 2 n :0012, 000112, 000122, v.v. Số 0 bằng tổng của không. của 1s và 2s. Tiếp tục đẩy các số 0 và khi gặp số 1 đầu tiên, sau đó bật các số 0 đó cho đến khi không còn số 1 nào. Sau đó, tiếp tục đẩy các số 0 một lần nữa và khi gặp 2 đầu tiên, sau đó bật các số 0 đó cho đến khi không còn 2s nào. Chuỗi sẽ được chấp nhận.
-
Chuỗi NULL cũng được chấp nhận. 0 0 1 0 2 0
Hãy hiểu máy
-
Chuyển đổi cho trạng thái q0:
-
0, I / 0I) - Nếu đỉnh của ngăn xếp là I và ký hiệu đầu vào hiện tại là 0 thì đẩy 0 lên trên cùng của ngăn xếp và giữ nguyên ở q0. Ngăn xếp trở thành 0I ...
-
(0, 0/00) - Nếu đỉnh của ngăn xếp là 0 và ký hiệu đầu vào hiện tại cũng là 0 thì đẩy 0 lên trên cùng của ngăn xếp và giữ nguyên ở q0. Ngăn xếp trở thành 00 .... Tiếp tục đẩy các số 0 cho đến 1 hoặc 2 tiếp theo
-
(1, 0 / $) - Nếu trên cùng của ngăn xếp là 0 và ký hiệu đầu vào hiện tại là 1 thì bật 0 và di chuyển đến q1.
-
(2, 0 / $) - Nếu đỉnh của ngăn xếp là 0 và ký hiệu đầu vào hiện tại là 2 thì bật 0 và di chuyển đến q2.
-
($, I / I) - Nếu đỉnh của ngăn xếp là I và không có đầu vào thì không làm gì cả và chuyển đến qf. Đối với chuỗi NULL.
-
-
Chuyển đổi cho trạng thái q1 -
-
(1, 0 / $) - Nếu đỉnh của ngăn xếp là 0 và ký hiệu đầu vào hiện tại là 1 thì bật 0 đến và giữ nguyên ở q1.
-
($, I / I) - Nếu trên cùng của ngăn xếp là I và không có đầu vào thì không làm gì cả và chuyển sang qf.
-
(2, 0 / $) - Nếu đỉnh của ngăn xếp là 0 và ký hiệu đầu vào hiện tại là 2 thì bật 0 và di chuyển đến q2.
-
-
Chuyển đổi cho trạng thái q2 -
-
(2, 0 / $) - Nếu đỉnh của ngăn xếp là 0 và ký hiệu đầu vào hiện tại là 2 thì bật 0 và giữ nguyên ở q2.
-
($, I / I) - Nếu trên cùng của ngăn xếp là I và không có đầu vào thì không làm gì cả và chuyển sang qf.
-
