Máy Turing - Máy Turing là một thiết bị được sử dụng để chấp nhận các từ của một ngôn ngữ được tạo ra bởi các ngữ pháp loại 0. Máy Turing (TM) là một mô hình toán học bao gồm một dải băng dài vô hạn được chia thành các ô mà đầu vào được đưa ra. Nó bao gồm một đầu đọc băng đầu vào. Một thanh ghi trạng thái lưu trữ trạng thái của máy Turing. Sau khi đọc một ký hiệu đầu vào, nó được thay thế bằng một ký hiệu khác, trạng thái bên trong của nó bị thay đổi và nó di chuyển từ ô này sang phải hoặc trái. Nếu TM đạt đến trạng thái cuối cùng, chuỗi đầu vào được chấp nhận, nếu không sẽ bị từ chối.
Một TM có thể được mô tả chính thức là 7 bộ (Q, X, Σ, δ, q0, B, F) trong đó -
- Q là một tập hợp hữu hạn các trạng thái
- X là bảng chữ cái trong băng
- Σ là bảng chữ cái đầu vào
- δ là một hàm chuyển tiếp; δ:Q × X → Q × X × {Left_shift, Right_shift}.
- q0 là trạng thái ban đầu
- B là ký hiệu trống
- F là tập hợp các trạng thái cuối cùng
Mục tiêu của chúng tôi là tạo ra một TM máy Turing chấp nhận ngôn ngữ
L =anbma (n + m) trong đó n, m> =1
Hãy để chúng tôi lấy ví dụ về những từ mà TM có thể chấp nhận,
- abaa, n =1, m =1
- aabaaa, n =2, m =1
- abbaaa, n =1, m =2
- aaabaaaa, n =3, m =1
Tức là n lần a, sau đó là m lần b, tiếp theo là n + m lần a. n, m> =1
Ít nhất là không. của a sẽ luôn là 3 và b là 1. Khi cả n =m =1.
Cách tiếp cận được tóm tắt bên dưới -
Đầu tiên máy chấp nhận tất cả n không. trong số a được theo sau bởi tất cả m không. của b’s. Sau đó, khi số a được đếm nhiều hơn, nó bắt đầu xóa các đầu vào b và a trước đó. Cuối cùng, khi không có một ký tự mới nào xuất hiện và phần đầu chạm đến ký tự đầu vào đầu tiên, điều đó có nghĩa là tất cả các ký tự đều được xử lý chính xác. Hãy để chúng tôi làm theo từng bước cho chuỗi đầu vào -
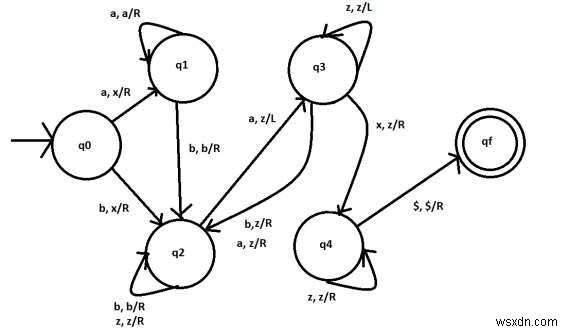
Chuyển đổi từ trạng thái q0
-
δ (q0, a) → (q1, x, R). Tại trạng thái q0 nếu ký tự đọc là một thì chuyển tiếp sang trạng thái q1, hãy làm cho nó x và di chuyển sang phải để trỏ ký tự tiếp theo trong chuỗi.
Ví dụ - aabaaa → xabaaa (ký tự đầu tiên trở thành x đầu được di chuyển sang phải tiếp theo a)
-
δ (q0, b) → (q3, x, R). Tại trạng thái q0 nếu ký tự được đọc là một sau đó chuyển sang trạng thái q3, hãy làm cho nó x và di chuyển sang phải để trỏ ký tự tiếp theo trong chuỗi.
Ví dụ - babaaa…. → xabaaa…. (ký tự đầu tiên trở thành x đầu di chuyển sang phải tiếp theo a)
Ở đây x được sử dụng để đại diện cho ký tự đầu tiên.
Chuyển đổi từ trạng thái q1
-
δ (q1, a) → (q1, a, R). Ở trạng thái q1 nếu ký tự được đọc là a thì vẫn ở trạng thái q1 và di chuyển sang phải để trỏ ký tự tiếp theo trong chuỗi.
Ví dụ:xaabaaa… → xaabaaa… (còn lại thì không làm gì cả và di chuyển sang phải)
-
δ (q1, b) → (q2, b, R). Ở trạng thái q1 nếu ký tự đọc là b thì vẫn ở trạng thái q1 và di chuyển sang phải để trỏ ký tự tiếp theo trong chuỗi.
Ví dụ - xaabaaa… → xaabaaa… (phần còn lại, b không làm gì và di chuyển sang phải)
Chuyển đổi từ trạng thái q2
-
δ (q2, b) → (q2, b, R). Ở trạng thái q2 nếu ký tự đọc là b thì vẫn ở trạng thái q2 và di chuyển sang phải để trỏ ký tự tiếp theo trong chuỗi.
Ví dụ - xaabbbaaa… → xaabbbaaa… (phần còn lại, b không làm gì cả và di chuyển sang phải)
-
δ (q2, z) → (q2, z, R). Ở trạng thái q2 nếu ký tự đọc là z thì vẫn ở trạng thái q2 và di chuyển sang phải để trỏ ký tự tiếp theo trong chuỗi.
Ví dụ - xaabaazz… → xaabaazz… (đối với phần còn lại, bạn không cần làm gì và di chuyển sang phải)
-
δ (q2, a) → (q3, z, L). Ở trạng thái q2 nếu ký tự được đọc là a, hãy chuyển nó thành z rồi chuyển sang trạng thái q3 và di chuyển sang trái để trỏ ký tự trước đó trong chuỗi.
Ví dụ - xaabaazz… → xaabazzz… (để thay thế a bằng z và di chuyển sang trái)
Chuyển đổi từ trạng thái q3
-
δ (q3, z) → (q3, z, L). Ở trạng thái q3 nếu ký tự đọc là z thì vẫn ở trạng thái q3 và di chuyển sang trái để trỏ ký tự trước đó trong chuỗi.
Ví dụ - xaabzzzz… → xaabzzzzz… (đối với z không làm gì cả và di chuyển sang trái)
-
δ (q3, b) → (q2, z, R). Tại trạng thái q2 nếu ký tự đọc là b thì chuyển nó thành z và chuyển tiếp tại trạng tháiq2 và di chuyển sang phải để trỏ ký tự tiếp theo trong chuỗi. Thay thế tất cả các b
Ví dụ - xaabzzzz… → xaazzzzz… (để thay thế b bằng z và di chuyển sang phải)
-
δ (q3, a) → (q2, z, R). Tại trạng thái q2 nếu ký tự được đọc là a thì chuyển nó thành z và chuyển sang trạng tháiq3, và di chuyển sang phải để trỏ ký tự tiếp theo trong chuỗi. Thay thế tất cả của a
Ví dụ - xaazzzz… → xaazzzzz… (thay thế a bằng z và di chuyển sang phải)
-
δ (q3, x) → (q4, z, R). Ở trạng thái q2 nếu ký tự đọc là x, hãy chuyển nó thành z sau đó chuyển sang trạng thái q3 và di chuyển sang phải để trỏ ký tự tiếp theo trong chuỗi. Biểu tượng đầu tiên đạt được.
Ví dụ - xzzzzzzz… → zzzzzzzz… (đối với x thay thế bằng z và di chuyển sang phải)
Chuyển đổi từ trạng thái q4
-
δ (q4, z) → (q4 z, R). Ở trạng thái q4 nếu ký tự đọc là z thì vẫn ở trạng thái q4 và di chuyển sang phải để trỏ ký tự tiếp theo trong chuỗi. Tất cả các ký tự bây giờ là z.
Ví dụ - zzzzzzzz… → zzzzzzzz… (đối với tất cả các z không làm gì cả và di chuyển sang phải)
-
δ (q4, $) → (qf, $, R). Ở trạng thái q4 nếu không có ký tự nào còn lại, đã đạt đến kết thúc. Chuyển tuyến đến qf cuối cùng. Có nghĩa là chuỗi được chấp nhận.
Ví dụ - zzzzzzzz $ → zzzzzzzz (đối với cuối chuỗi, $ không làm gì cả và chuyển đến trạng thái cuối cùng)
Sơ đồ cho thấy máy điều chỉnh -
Đầu vào
aabaaa q0: aabaaa → q1: xabaaa → q1: xabaaa → q2: xabaaa → q3: xabzaa → q2: xazzaa q2: xazzaa → q3: xazzza → q3: xazzza → q3: xazzza → q2: xzzzzza → q2: xzzzzza q2: xzzzzza → q2: xzzzzza → q2: xzzzzza → q2: xzzzzzz → q3: xzzzzzz…….. q3: xzzzzzz → q3: xzzzzzz → q4: zzzzzzz → q4: zzzzzzz…….q4: xzzzzzz$ → qf: xzzzzzz$
Đạt đến qf nghĩa là aabaaa được chấp nhận
