In các khóa BST trong Dải ô đã cho - Khoảng trống O (1) trong C ++

Trong bài toán này, chúng ta được cung cấp hai giá trị k1 và k2 (k1 In các khóa BST trong Phạm vi đã cho.

Mô tả sự cố: Chúng tôi sẽ in tất cả các khóa của cây từ n1 đến n2 theo thứ tự tăng dần.

Hãy lấy một ví dụ để hiểu vấn đề,

Đầu vào:

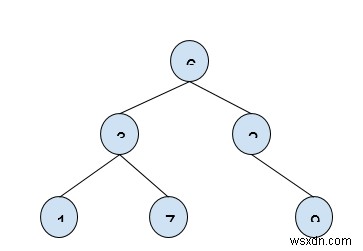
k1 =4, k2 =12

Đầu ra: 6, 7, 9

Phương pháp tiếp cận giải pháp

Đơn giản, chúng tôi có thể giải quyết vấn đề bằng cách sử dụng inorder traversal nhưng độ phức tạp không gian ở đó là 0 (n) nhưng nhu cầu của giờ là giải quyết độ phức tạp O (1). Vì vậy, đối với điều này, chúng tôi sẽ sử dụng một loại kỹ thuật di chuyển đặc biệt.

Chúng tôi sẽ sử dụng Morris Traversal dựa trên cây nhị phân luồng. Nó không yêu cầu bất kỳ ngăn xếp / hàng đợi nào và sử dụng con trỏ NULL để lưu trữ thông tin, điều này giúp giảm dung lượng lưu trữ xuống O (1).

Chương trình minh họa hoạt động của morris traversal để giải quyết vấn đề,

Ví dụ

#include <iostream>
using namespace std;

struct node {
   int data;
   struct node *left, *right;
};

node* insertNode(int data) {
   node* temp = new node;
   temp->data = data;
   temp->right = temp->left = NULL;
   return temp;
}

void RangeTraversal(node* root, int k1, int k2) {
   
   if (!root)
      return;
     
   node* nodeTraversal = root;

   while (nodeTraversal) {

      if (nodeTraversal->left == NULL) {

         if (nodeTraversal->data <= k2 &amp;&amp; nodeTraversal->data >= k1)
         
            cout<<nodeTraversal->data<<" ";
         nodeTraversal = nodeTraversal->right;
      }

      else {
         node* prevNode = nodeTraversal->left;
         while (prevNode->right != NULL &amp;&amp; prevNode->right != nodeTraversal)
            prevNode = prevNode->right;

         if (prevNode->right == NULL) {
            prevNode->right = nodeTraversal;
            nodeTraversal = nodeTraversal->left;
         }
         else {
            prevNode->right = NULL;
            if (nodeTraversal->data <= k2 &amp;&amp; nodeTraversal->data >= k1)
               cout<<nodeTraversal->data<<" ";
            nodeTraversal = nodeTraversal->right;
         }
      }
   }
}

int main() {
   node* root = insertNode(6);
   root->left = insertNode(3);
   root->right = insertNode(2);
   root->left->left = insertNode(1);
   root->left->right = insertNode(7);
   root->right->right = insertNode(9);

   cout<<"All BST keys in the given range are \t";
   RangeTraversal(root, 4, 10);
   
   return 0;
}

Đầu ra

All BST keys in the given range are 7 6 9