Tích các thừa số nguyên tố duy nhất của một số trong Chương trình Python

Trong bài viết này, chúng ta sẽ tìm hiểu về giải pháp cho câu lệnh vấn đề được đưa ra bên dưới -

Tuyên bố vấn đề

Cho một số n, chúng ta cần tìm tích của tất cả các thừa số nguyên tố duy nhất có sẵn của nó và trả về.

Ví dụ

Input: num = 11
Output: Product is 11

Giải thích

Ở đây, số đầu vào là 11 chỉ có 1 thừa số nguyên tố và nó là 11. Và do đó tích của chúng là 11.

Cách tiếp cận 1

Sử dụng vòng lặp for từ i =2 đến n + 1 để kiểm tra xem tôi có phải là thừa số của n hay không và sau đó kiểm tra xem tôi có phải là số nguyên tố hay không, nếu có thì lưu trữ sản phẩm trong biến sản phẩm và tiếp tục quá trình này cho đến khi tôi trở thành =n.

Ví dụ

def productPrimeFactors(n):
   product = 1
   for i in range(2, n+1):
      if (n % i == 0):
         isPrime = 1
         for j in range(2, int(i/2 + 1)):
            if (i % j == 0):
               isPrime = 0
               break
      if (isPrime):
         product = product * i
   return product
# main
n = 18
print (productPrimeFactors(n))

Đầu ra

120

Phạm vi của tất cả các biến được hiển thị trong hình ảnh bên dưới -

Cách tiếp cận 2

1) Trong khi n chia hết cho 2 (chẵn) thì in ra 2 và chia n cho 2.

2) Sau bước 1, n phải trở thành số lẻ. Bây giờ bắt đầu một vòng lặp for từ i =3 cho đến căn bậc hai của n. Trong khi tôi chia n, in ra i và chia n cho i. Sau khi tôi không chia được n, hãy tăng i cho 2 và tiếp tục quá trình.

3) Nếu n là một số nguyên tố và lớn hơn 2, thì n sẽ không trở thành 1 trong hai bước trên. Do đó in n nếu nó lớn hơn 2.

Ví dụ

import math
def productPrimeFactors(n):
   product = 1
   # prime factor 2
   if (n % 2 == 0):
      product *= 2
      while (n%2 == 0):
         n = n/2
   # n must be odd
   for i in range (3, int(math.sqrt(n)), 2):
      # While i divides n, print i and
      # divide n
      if (n % i == 0):
         product = product * i
         while (n%i == 0):
            n = n/i
   # n is a prime number greater than 2
   if (n > 2):
      product = product * n
   return product
# main()
n = 8
print (int(productPrimeFactors(n)))

Đầu ra

2

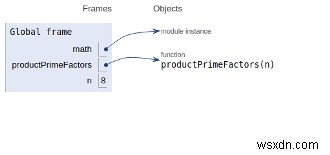
Phạm vi của các biến được đề cập trong hình ảnh bên dưới -

Kết luận

Trong bài viết này, chúng ta đã tìm hiểu về tích các thừa số nguyên tố duy nhất của một số nhất định với phương pháp tiếp cận bạo lực và phương pháp tiếp cận hiệu quả