Computer >> Máy Tính >  >> Lập trình >> Python

Các cạnh tối thiểu bắt buộc phải thêm để tạo nên Mạch Euler trong Python

Giả sử chúng ta có một đồ thị vô hướng gồm b số nút và một số cạnh; chúng ta phải tìm các cạnh tối thiểu cần thiết để tạo Mạch Euler trong biểu đồ này.

Vì vậy, nếu đầu vào giống như

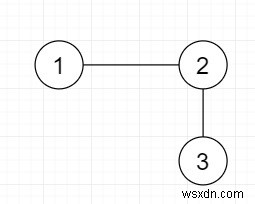
Các cạnh tối thiểu bắt buộc phải thêm để tạo nên Mạch Euler trong Python

thì đầu ra sẽ là 1.

Để giải quyết vấn đề này, chúng tôi sẽ làm theo các bước sau -

  • Định nghĩa một hàm dfs (). Điều này sẽ lấy g, thăm, lẻ_vert, độ, tổng hợp, v
  • truy cập [v]:=1
  • nếu độ [v] mod 2 giống với 1, thì
    • retail_vert [comp]:=retail_vert [comp] + 1
  • đối với u trong phạm vi từ 0 đến kích thước là g [v], hãy thực hiện
    • nếu lượt truy cập [u] giống 0, thì
      • dfs (g, visit, retail_vert, Deg, comp, u)
  • Từ phương thức chính, hãy làm như sau -
  • g:=một danh sách gồm n + 1 danh sách trống
  • e:=một danh sách mới
  • :=một danh sách mới
  • độ:=danh sách kích thước mới (n + 1) và điền bằng 0
  • visit:=danh sách kích thước mới (n + 1) và điền bằng 0
  • lẻ_vert:=danh sách kích thước mới (n + 1) và điền
  • với 0
  • đối với tôi trong phạm vi từ 0 đến m, thực hiện
    • chèn d [i] vào cuối g [s [i]]
    • chèn s [i] vào cuối g [d [i]]
    • độ [s [i]]:=độ [s [i]] + 1
    • độ [d [i]]:=độ [d [i]] + 1
  • ans:=0, comp:=0
  • đối với tôi trong phạm vi từ 1 đến n + 1, hãy thực hiện
    • nếu lượt truy cập [i] giống 0, thì
      • comp:=comp + 1
      • dfs (g, visit, retail_vert, Degree, comp, i)
      • nếu retail_vert [comp] giống 0, thì
        • chèn comp vào cuối e
      • nếu không,
        • chèn comp vào cuối o
  • nếu kích thước của o bằng 0 và kích thước của e bằng 1, thì
    • trả về 0
  • nếu kích thước của o bằng 0, thì
    • trả về kích thước của e
  • nếu kích thước của e không bằng 0, thì
    • ans:=ans + kích thước của e
  • đối với tôi trong phạm vi từ 0 đến kích thước là o, thực hiện
    • ans:=ans + retail_vert [i] / 2 (chỉ lấy phần nguyên)
  • trả lại ans

Ví dụ

Hãy cùng chúng tôi xem cách triển khai sau để hiểu rõ hơn - 

def dfs(g, visit, odd_vert, degree, comp, v):
   visit[v] = 1
   if (degree[v] % 2 == 1):
      odd_vert[comp] += 1
   for u in range(len(g[v])):
      if (visit[u] == 0):
         dfs(g, visit, odd_vert, degree, comp, u)
def solve(n, m, s, d):
   g = [[] for i in range(n + 1)]
   e = []
   o = []
   degree = [0] * (n + 1)
   visit = [0] * (n + 1)
   odd_vert = [0] * (n + 1)
   for i in range(m):
      g[s[i]].append(d[i])
      g[d[i]].append(s[i])
      degree[s[i]] += 1
      degree[d[i]] += 1
   ans = 0
   comp = 0
   for i in range(1, n + 1):
      if (visit[i] == 0):
         comp += 1
         dfs(g, visit, odd_vert, degree, comp, i)
         if (odd_vert[comp] == 0):
            e.append(comp)
         else:
            o.append(comp)
   if (len(o) == 0 and len(e) == 1):
      return 0
   if (len(o) == 0):
      return len(e)
   if (len(e) != 0):
      ans += len(e)
   for i in range(len(o)):
      ans += odd_vert[i] // 2
   return ans
b = 3
a = 2
source = [ 1, 2 ]
destination = [ 2, 3]
print(solve(b, a, source, destination))

Đầu vào 

b = 3 a = 2 source = [ 1, 2 ] destination = [ 2, 3]

Đầu ra 

1