Giả sử chúng ta có một số n, chúng ta phải tìm hàng thứ n (có chỉ số 0) của tam giác Pascal. Như chúng ta đã biết, tam giác Pascal có thể được tạo như sau -
- Ở hàng trên cùng, có một mảng 1.
- Hàng tiếp theo được thực hiện bằng cách thêm số ở trên và bên trái với số hiệu và ở bên phải.
Vì vậy, một số hàng như sau -
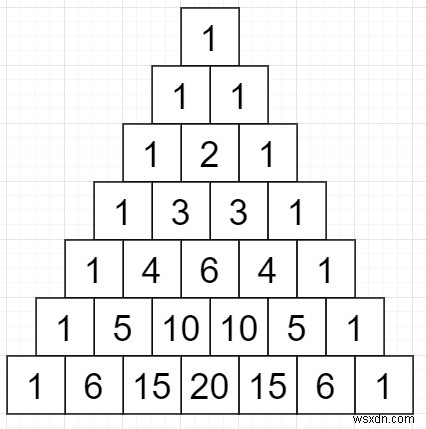
Vì vậy, nếu đầu vào là 4, thì đầu ra sẽ là [1, 4, 6, 4, 1]
Để giải quyết vấn đề này, chúng tôi sẽ làm theo các bước sau -
- nếu n giống 0, thì
- trả lại [1]
- nếu n giống 1, thì
- trả về [1,1]
- ls:=danh sách có [1,1], temp:=danh sách có [1,1]
- đối với tôi trong phạm vi từ 2 đến n + 1, hãy thực hiện
- ls:=temp
- temp:=danh sách có một giá trị =1
- đối với tôi trong phạm vi 0 đến kích thước ls -1, thực hiện
- hợp nhất ls [i], ls [i + 1] và chèn vào cuối tạm thời
- chèn 1 vào cuối nhiệt độ
- nhiệt độ trở lại
Hãy cùng chúng tôi xem cách triển khai sau để hiểu rõ hơn -
Ví dụ
class Solution: def solve(self, n): if n==0: return [1] if n==1: return [1,1] ls=[1,1] temp=[1,1] for i in range(2,n+1): ls=temp temp=[1] for i in range(len(ls)-1): temp.append(ls[i]+ls[i+1]) temp.append(1) return temp ob = Solution() print(ob.solve(4))
Đầu vào
4
Đầu ra
[1, 4, 6, 4, 1]
