Giả sử chúng ta có một rô bốt, hiện đang ngồi ở vị trí (0, 0) (Mặt phẳng Descartes). Nếu chúng ta có danh sách các bước di chuyển của nó mà nó có thể thực hiện, bao gồm N (Bắc), S (Nam), W (Tây) và E (Đông). Tuy nhiên, nếu rô-bốt đến vị trí đã đến trước đó, thì rô-bốt sẽ tiếp tục di chuyển theo hướng cũ cho đến khi đến vị trí mới không có người mong đợi. Chúng tôi phải kiểm tra xem sau khi di chuyển, nó có kết thúc ở tọa độ (x, y) hay không.
Vì vậy, nếu đầu vào giống như
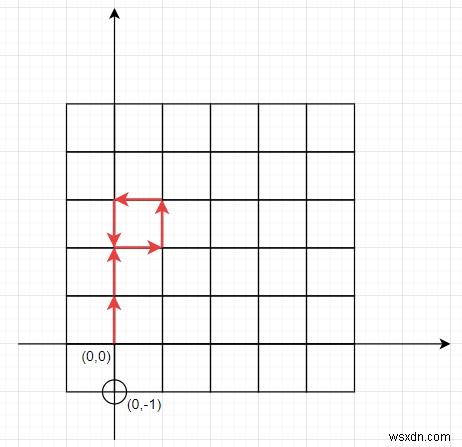
Move =['N', 'N', 'E', 'N', 'W', 'S'], coord =[0, -1], thì đầu ra sẽ là True, vì robot sẽ đi hai bước lên, một phải, lại lên, một trái và một xuống, khi vị trí hiện tại được truy cập, nó sẽ đi xuống, sau đó địa điểm đó cũng được truy cập, lại đi xuống, vì vậy dừng lại ở vị trí (0, −1)
Để giải quyết vấn đề này, chúng tôi sẽ làm theo các bước sau -
-
ny:=0, nx:=0
-
l:=một tập hợp mới, ban đầu chèn tọa độ (0, 0)
-
đối với mỗi k trong nước đi, hãy thực hiện
-
nếu k giống với "N" thì
-
while (nx, ny) trong l, do
-
ny:=ny + 1
-
-
-
ngược lại khi k giống "S" thì
-
while (nx, ny) trong l, do
-
ny:=ny - 1
-
-
-
ngược lại khi k giống "E" thì
-
while (nx, ny) trong l, do
-
nx:=nx + 1
-
-
-
nếu không,
-
while (nx, ny) trong l, do
-
nx:=nx - 1
-
-
-
thêm (nx, ny) vào l
-
-
trả về true khi coord giống như (nx, ny), ngược lại là false
Hãy cùng chúng tôi xem cách triển khai sau để hiểu rõ hơn -
Ví dụ
class Solution:
def solve(self, moves, coord):
ny = nx = 0
l = {(0, 0)}
for k in moves:
if k == "N":
while (nx, ny) in l:
ny += 1
elif k == "S":
while (nx, ny) in l:
ny -= 1
elif k == "E":
while (nx, ny) in l:
nx += 1
else:
while (nx, ny) in l:
nx -= 1
l.add((nx, ny))
return coord[0] == nx and coord[1] == ny
ob = Solution()
moves = ['N','N','E','N','W','S']
coord = [0,-1]
print(ob.solve(moves, coord)) Đầu vào
['N','N','E','N','W','S'], [0,-1]
Đầu ra
True
