Giả sử chúng ta có một ma trận nhị phân N x N trong đó 0 là ô trống và 1 là ô bị chặn, chúng ta phải tìm số cách chọn N ô trống sao cho mọi hàng và mọi cột đều có ít nhất một ô được chọn. Nếu câu trả lời là rất lớn, kết quả trả về mod 10 ^ 9 + 7
Vì vậy, nếu đầu vào giống như
| 0 | 0 | 0 |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
thì đầu ra sẽ là 4, vì chúng ta có các cấu hình sau (trong đó x là ô được chọn) -
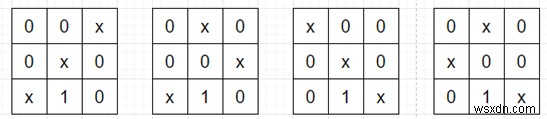
Để giải quyết vấn đề này, chúng tôi sẽ làm theo các bước sau -
- n:=kích thước của ma trận
- Định nghĩa một hàm f (). Điều này sẽ mất tôi, bs
- nếu tôi> =n, thì
- trả lại 1
- ans:=0
- đối với j trong phạm vi từ 0 đến n, thực hiện
- nếu ma trận [i, j] giống 0 và (2 ^ j VÀ bs giống 0), thì
- ans:=ans + f (i + 1, bs OR 2 ^ j)
- nếu ma trận [i, j] giống 0 và (2 ^ j VÀ bs giống 0), thì
- trả lại ans
- Từ lệnh gọi phương thức chính và trả về f (0, 0)
Hãy cùng chúng tôi xem cách triển khai sau để hiểu rõ hơn -
Ví dụ
class Solution: def solve(self, matrix): n = len(matrix) def f(i, bs): if i >= n: return 1 ans = 0 for j in range(n): if matrix[i][j] == 0 and ((1 << j) & bs == 0): ans += f(i + 1, bs | (1 << j)) return ans return f(0, 0) ob = Solution() matrix = [ [0, 0, 0], [0, 0, 0], [0, 1, 0] ] print(ob.solve(matrix))
Đầu vào
[ [0, 0, 0], [0, 0, 0], [0, 1, 0] ]
Đầu ra
4
