Chương trình tìm số màu tối thiểu còn lại sau khi hợp nhất bằng Python

Giả sử chúng ta có một danh sách các màu (R, G, B). Bây giờ nếu hai màu khác nhau ở cạnh nhau thì chúng có thể biến đổi thành một mục màu duy nhất của màu thứ ba. Chúng ta phải tìm số lượng nhỏ nhất còn lại sau bất kỳ chuỗi biến đổi nào có thể xảy ra.

Vì vậy, nếu đầu vào giống như color =["G", "R", "G", "B", "R"], thì đầu ra sẽ là 1 vì nó có thể biến đổi như bên dưới -

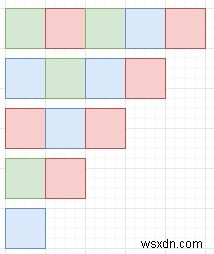
Để giải quyết vấn đề này, chúng tôi sẽ làm theo các bước sau -

• n:=kích thước của màu sắc
• nếu các màu chỉ có một màu riêng biệt, thì
  • return n
• nếu n <=1, thì
  • return n
• x:=0
• d:=một bản đồ với các cặp giá trị khóa {("R", 1), ("G", 2), ("B", 3)}
• đối với mỗi c trong các màu, thực hiện
  • x:=x XOR d [c]
• trả về 2 nếu x giống với 0 nếu không thì 1

Ví dụ (Python)

Hãy cùng chúng tôi xem cách triển khai sau để hiểu rõ hơn -

class Solution:
   def solve(self, colors):
      n = len(colors)
      if len(set(colors)) == 1:
         return n
      if n <= 1:
         return n
      x = 0
      d = {"R": 1, "G": 2, "B": 3}
      for qux in colors:
         x ^= d[qux]
      return 2 if x == 0 else 1   
ob = Solution()
colors = ["G", "R", "G", "B", "R"]
print(ob.solve(colors))

Đầu vào

["G", "R", "G", "B", "R"]

Đầu ra

1