Giả sử chúng ta có một danh sách các cạnh ở dạng (u, v) và các cạnh này đại diện cho một cây. Đối với mỗi cạnh, chúng ta phải tìm tổng số đường dẫn duy nhất bao gồm cạnh đã nói, theo thứ tự như đã cho trong đầu vào.
Vì vậy, nếu đầu vào giống như các cạnh =[[0, 1], [0, 2], [1, 3], [1, 4]]
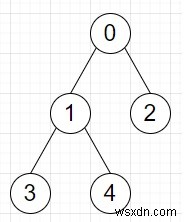
thì đầu ra sẽ là [6, 4, 4, 4].
Để giải quyết vấn đề này, chúng tôi sẽ làm theo các bước sau -
-
adj:=danh sách kề từ các cạnh đã cho
-
count:=một bản đồ trống
-
Định nghĩa một hàm dfs (). Điều này sẽ lấy x, cha mẹ
-
đếm [x]:=1
-
đối với mỗi nb trong adj [x], thực hiện
-
nếu nb giống với cha mẹ thì
-
đi ra từ vòng lặp
-
-
count [x]:=count [x] + dfs (nb, x)
-
-
số lượng trả về [x]
-
Từ phương thức chính, hãy làm như sau -
-
dfs (0, -1)
-
ans:=một danh sách mới
-
đối với mỗi cạnh (a, b) trong các cạnh, thực hiện
-
x:=số đếm tối thiểu [a] và số đếm [b]
-
insert (x * (count [0] - x)) vào cuối ans
-
-
trả lại ans
Ví dụ
Hãy cùng chúng tôi xem cách triển khai sau để hiểu rõ hơn -
from collections import defaultdict class Solution: def solve(self, edges): adj = defaultdict(list) for a, b in edges: adj[a].append(b) adj[b].append(a) count = defaultdict(int) def dfs(x, parent): count[x] = 1 for nb in adj[x]: if nb == parent: continue count[x] += dfs(nb, x) return count[x] dfs(0, -1) ans = [] for a, b in edges: x = min(count[a], count[b]) ans.append(x * (count[0] - x)) return ans ob = Solution() edges = [ [0, 1], [0, 2], [1, 3], [1, 4] ] print(ob.solve(edges))
Đầu vào
[ [0, 1], [0, 2], [1, 3], [1, 4] ]
Đầu ra
[6, 4, 4, 4]
