Kiểm tra xem chuỗi nhị phân có bội số 3 hay không bằng cách sử dụng DFA trong Python

Giả sử chúng ta có một mảng n biểu diễn một biểu diễn nhị phân của một số bất kỳ. Chúng ta phải kiểm tra xem biểu diễn nhị phân của nó có chia hết cho ba hay không bằng cách sử dụng DFA dữ liệu tự động hữu hạn xác định.

Vì vậy, nếu đầu vào là n =[1, 1, 0, 0] (nhị phân của 12), thì đầu ra sẽ là True.

Để giải quyết vấn đề này, chúng ta có thể xây dựng DFA như bên dưới -

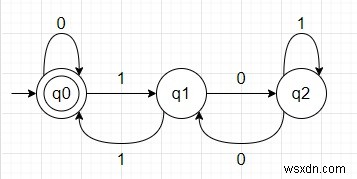
Cách tiếp cận rất đơn giản khi một số chia hết cho 3 thì phần dư sẽ là 0, nếu không thì phần dư sẽ là 1 hoặc 2. Có ba trạng thái cho ba phần dư này. Trạng thái ban đầu cũng là trạng thái cuối cùng vì khi phần dư bằng 0 có nghĩa là số đó có thể chia hết.

Để giải quyết vấn đề này, chúng tôi sẽ làm theo các bước sau -

• dfa_state:=0
• đối với tôi trong phạm vi từ 0 đến kích thước là nums - 1, thực hiện
  • chữ số:=nums [i]
  • nếu dfa_state là 0, thì
    • nếu chữ số giống 1, thì
      • dfa_state:=1
  • ngược lại khi dfa_state là 1 thì
    • nếu chữ số giống 0, thì
      • dfa_state:=2
    • nếu không,
      • dfa_state:=0
  • ngược lại khi dfa_state là 2 thì
    • nếu chữ số giống 0, thì
      • dfa_state:=1
• nếu dfa_state là 0, thì
  • trả về True
• trả về Sai

Hãy cùng chúng tôi xem cách triển khai sau để hiểu rõ hơn -

Ví dụ

def solve(nums):
   dfa_state = 0
   for i in range(len(nums)):
      digit = nums[i]
      if dfa_state == 0:
         if digit == 1:
            dfa_state = 1
         elif dfa_state == 1:
            if digit == 0:
               dfa_state = 2
            else:
               dfa_state = 0
         elif dfa_state == 2:
            if digit == 0:
               dfa_state = 1
            if dfa_state == 0:
               return True
   return False
n = [1, 1, 0, 0]
print(solve(n))

Đầu vào

[1, 1, 0, 0]

Đầu ra

True