Giả sử chúng ta có một số n. Chúng ta phải kiểm tra xem n có phải là số quặng hay không. Như chúng ta biết một số quặng là một số có ước của nó là một giá trị hài nguyên.
Vì vậy, nếu đầu vào là 28, thì đầu ra sẽ là Đúng vì có sáu ước của 28:[1, 2, 4, 7, 14, 28], vì vậy
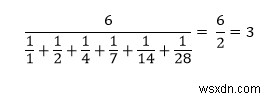
Vì 3 là một số nguyên nên 28 là một số quặng.
Để giải quyết vấn đề này, chúng tôi sẽ làm theo các bước sau -
- Xác định một hàm get_all_div (). Điều này sẽ mất n
- div:=một danh sách mới
- đối với tôi trong phạm vi từ 1 đến phần nguyên của (căn bậc hai của n), hãy thực hiện
- nếu n chia hết cho i thì
- nếu thương của (n / i) là i, thì
- chèn i vào cuối div
- nếu không,
- chèn i vào cuối div
- chèn thương số của (n / i) vào cuối div
- nếu thương của (n / i) là i, thì
- nếu n chia hết cho i thì
- trả về div
- Xác định một hàm get_harmonic_mean (). Điều này sẽ mất n
- div:=get_all_div (n)
- tổng số:=0
- length:=kích thước của div
- đối với tôi trong phạm vi 0 đến length - 1, thực hiện
- tổng số:=tổng số + (n / div [i])
- tổng số:=tổng số / n
- chiều dài / tổng số trả về
- Từ phương thức chính, hãy làm như sau:
- nghĩa là:=get_harmonic_mean (n)
- nếu giá trị trung bình là một số nguyên, thì
- trả về True
- trả về Sai
Hãy cùng chúng tôi xem cách triển khai sau để hiểu rõ hơn -
Mã mẫu
def get_all_div(n): div = [] for i in range(1, int(n**(0.5)) + 1): if n % i == 0: if n // i == i: div.append(i) else: div.append(i) div.append(n // i) return div def get_harmonic_mean(n): div = get_all_div(n) total = 0 length = len(div) for i in range(0, length): total += (n / div[i]) total /= n return length / total def solve(n): mean = get_harmonic_mean(n) if mean - int(mean) == 0: return True return False n = 28 print(solve(n))
Đầu vào
28
Đầu ra
True
