Chương trình Python để tạo một cây biểu thức của một biểu thức nhất định

Cây biểu thức là những cây trong đó các nút lá có giá trị được vận hành và các nút bên trong chứa toán tử mà trên đó nút lá sẽ được thực hiện.

Ví dụ:4 + ((7 + 9) * 2) sẽ có một cây biểu thức như -

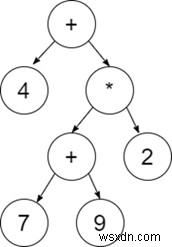
Phương pháp tiếp cận để giải quyết vấn đề này

Để xây dựng Cây biểu thức cho một biểu thức nhất định, chúng ta thường sử dụng Cấu trúc dữ liệu ngăn xếp. Ban đầu, chúng tôi Lặp lại biểu thức postfix đã cho và làm theo các bước như dưới đây -

• Nếu chúng ta nhận được một toán hạng trong biểu thức đã cho, thì hãy đẩy nó vào ngăn xếp. Nó sẽ trở thành gốc của Cây biểu thức.
• Nếu một toán tử nhận được hai giá trị trong biểu thức, thì hãy thêm vào cây biểu thức làm con của nó và đẩy chúng vào nút hiện tại.
• Lặp lại Bước-1 và Bước-2 cho đến khi chúng tôi không hoàn thành biểu thức đã cho của mình.

Ví dụ

class stack:
   def __init__(self):
      self.arr = []
   def push(self, data):
      self.arr.append(data)
   def pop(self):
      try:
         return self.arr.pop(-1)
      except:
         pass
   def top(self):
      try:
         return self.arr[-1]
      except:
         pass
   def size(self):
      return len(self.arr)
# node class for expression tree
class node:
   def __init__(self, data):
      self.data = data
      self.left = None
      self.right = None
# expression tree class
class exp_tree:
   def __init__(self, postfix_exp):
      self.exp = postfix_exp
      self.root = None
      self.createTree(self.exp)
   def isOperator(self, char):
      optr = [" ", "-", "*", "/", "^"]
      if char in optr: # if given char is operator
         return True # then return true
      return False # else return false
   def createTree(self, exp):
      s = stack()
      # store those operator node whose any child node is NULL
      self.root = node(exp[-1])
      # last character of postfix expression is always an operator
      s.push(self.root)
      # travel on rest of the postfix expression
      for i in "".join(reversed(exp[:-1])):
         curr_node = s.top()
         if not curr_node.right:
            # if right node of current node is NULL
            temp = node(i)
            curr_node.right = temp
            if self.isOperator(i):
               s.push(temp)
         else: # if left node of current node is NULL
            temp = node(i)
            curr_node.left = temp
            # if no child node of current node is NULL
            s.pop() # pop current from stack
            if self.isOperator(i):
               s.push(temp)
   def inorder(self, head):
      # inorder traversal of expression tree
      # inorder traversal = > left, root, right
      if head.left:
         self.inorder(head.left)
      print(head.data, end=" ")
      if head.right:
         self.inorder(head.right)
   def infixExp(self):
      # inorder traversal of expression tree give infix expression
      self.inorder(self.root)
      print()
if __name__ == "__main__":
   postfixExp = "ab ef*g*-"
   et = exp_tree(postfixExp)
   et.infixExp()

Chạy đoạn mã trên sẽ tạo ra kết quả là,

Đầu ra

(a + b - e * f * g)

Giải thích:

Việc tạo cây từ một biểu thức đã cho sẽ tạo ra kết quả sao cho toán hạng sẽ trở thành gốc của nút và phần còn lại của các số sẽ trở thành nút con của cây biểu thức.