Chương trình Python để tìm số lượng hoạt động để đóng gói một số thanh kim loại trong một thùng chứa

Giả sử, chúng ta được giao nhiệm vụ vận chuyển một số thanh kim loại có kích thước khác nhau. Nhưng container vận chuyển có chiều dài ngắn, có thể chứa các thanh có chiều dài 1 chỉ. Chúng tôi được cung cấp n số thanh, và độ dài của chúng được cung cấp cho chúng tôi trong một danh sách. Vì vậy, để lắp tất cả các thanh trong thùng chứa; chúng ta phải cắt và chia tất cả các thanh để chúng có kích thước đơn vị. Hơn nữa, chúng tôi lắp tất cả các thanh vào thùng chứa mà chi phí cho chúng tôi một lần hoạt động. Chúng tôi phải tìm số lượng hoạt động chúng tôi phải thực hiện trên các thanh.

Vì vậy, nếu đầu vào là input_arr =[6, 3, 7], thì đầu ra sẽ là 22

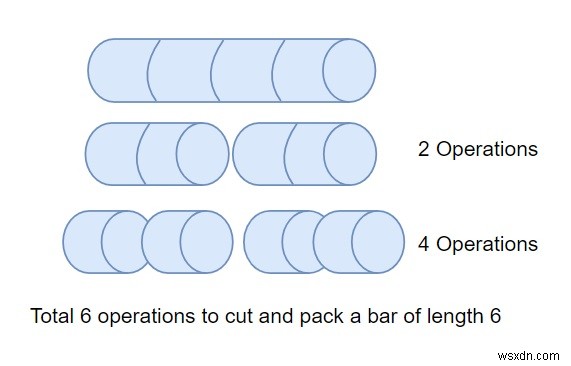
Để biến thanh có kích thước 6 thành thanh có kích thước 1, chúng ta phải thực hiện 10 thao tác.
Để biến thanh có kích thước 3 thành thanh có kích thước 1, chúng ta phải thực hiện 4 thao tác.
Để biến thanh có kích thước 7 thành thanh có kích thước 1, chúng ta phải thực hiện 8 thao tác.

Để giải quyết vấn đề này, chúng tôi sẽ làm theo các bước sau -

Định nghĩa một hàm prime_find (). Điều này sẽ lấy input_num
- prime_check:=một danh sách mới có kích thước giá trị sàn là ((input_num-1) / 2) chứa giá trị True
- cho p_num trong phạm vi 3 đến tầng của căn bậc hai của (input_num) +1, tăng 2, thực hiện
  - nếu prime_check [giá trị sàn của (p_num-3) / 2] khác 0 thì
    - đối với mỗi phần tử trong phạm vi giá trị sàn từ (p_num ^ 2-3) / 2 đến p_num trong prime_check, thực hiện
      - prime_check [element]:=một danh sách mới có kích thước (giá trị sàn của ((input_num-p_num ^ 2) / (2 * p_num) + 1)) chứa giá trị False
- đối với tôi trong phạm vi từ 0 đến giá trị sàn của (input_num - 1) / 2, thực hiện
  - nếu prime_check [i] là True -
    - trả về danh sách chứa các giá trị 2 + 2 * i + 3
Từ chức năng chính, thực hiện như sau -
- prime_nums:=prime_find (10 ^ 6 + 100)
- kết quả:=0
- đối với mỗi giá trị trong input_arr, hãy thực hiện
  - kết quả:=kết quả + giá trị
  - f_list:=một danh sách mới
  - đối với mỗi p_num trong prime_nums, thực hiện
    - trong khi giá trị mod p_num giống 0, hãy thực hiện
      - chèn p_num vào cuối f_list
      - giá trị:=giá trị sàn của (value / p_num)
    - if p_num ^ 2> value, then
      - nếu giá trị> 1, thì
        
        chèn giá trị vào cuối f_list
      - thoát khỏi vòng lặp
  - - tạm thời:=1
    - đối với mỗi p_num trong f_list theo thứ tự ngược lại, hãy thực hiện
      - kết quả:=kết quả + tạm thời
      - temp:=temp * p_num
- trả về kết quả

Ví dụ

Hãy cùng chúng tôi xem cách triển khai sau để hiểu rõ hơn -

from math import floor,sqrt
def prime_find(input_num):
   prime_check = [True]*((input_num-1)//2)
   for p_num in range(3,floor(sqrt(input_num))+1,2):
      if prime_check[(p_num-3)//2]: prime_check[(p_num**2-3)//2::p_num] = [False] * ((input_num-p_num**2)//(2*p_num) + 1)
   return [2]+[2*i+3 for i in range((input_num - 1) // 2) if prime_check[i]]
def solve(input_arr):
   prime_nums = prime_find(10**6+100)
   result = 0
   for value in input_arr:
      result += value
      f_list = []
      for p_num in prime_nums:
         while value % p_num == 0:
            f_list.append(p_num)
            value //= p_num
         if p_num**2 > value:
            if value > 1:
               f_list.append(value)
         break
      temp = 1
      for p_num in f_list[-1::-1]:
         result += temp
         temp *= p_num
   return result
if __name__ == "__main__":
print(solve([6, 3, 7]))

Đầu vào

[6, 3, 7]

Chương trình Python để tìm số lượng hoạt động để đóng gói một số thanh kim loại trong một thùng chứa

Ví dụ

Đầu vào

Đầu ra