Giả sử chúng ta có hai mảng nums1 và nums2. Đường dẫn hợp lệ được xác định như sau -
-
Chọn nums1 hoặc nums2 để duyệt (từ index-0).
-
Di chuyển mảng từ trái sang phải.
Bây giờ, nếu chúng ta đang di chuyển qua bất kỳ giá trị nào có trong nums1 và nums2, chúng ta có thể thay đổi đường dẫn đến mảng khác. Ở đây điểm là tổng các giá trị duy nhất trong một đường dẫn hợp lệ. Chúng tôi phải tìm điểm tối đa mà chúng tôi có thể nhận được trong tất cả các con đường hợp lệ có thể có. Nếu câu trả lời quá lớn thì trả về mô đun kết quả 10 ^ 9 + 7.
Vì vậy, nếu đầu vào giống như nums1 =[3,5,6,9,11] nums2 =[5,7,9,10], thì đầu ra sẽ là 35 vì -
-
Các đường dẫn hợp lệ bắt đầu từ nums1 là:[3,5,6,9,11], [3,5,6,9,10], [3,5,7,9,10], [3,5,7, 9,11]
-
Các đường dẫn hợp lệ bắt đầu từ nums2 là:[5,7,9,10], [5,6,9,11], [5,6,9,10], [5,7,9,11]
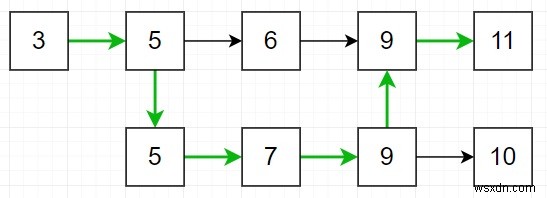
Vì vậy, tối đa là [3,5,7,9,11].
Để giải quyết vấn đề này, chúng tôi sẽ làm theo các bước sau -
-
M:=kích thước của nums1, N:=kích thước của nums2
-
sum1:=0, sum2:=0
-
i:=0, j:=0
-
res:=0
-
trong khi tôi
-
nếu nums1 [i]
-
sum1:=sum1 + nums1 [i]
-
i:=i + 1
-
-
ngược lại khi nums1 [i]> nums2 [j] thì
-
sum2:=sum2 + nums2 [j]
-
j:=j + 1
-
-
nếu không,
-
res:=res + tối đa của sum1, (sum2 + nums1 [i])
-
i:=i + 1
-
j:=j + 1
-
sum1:=0
-
sum2:=0
-
-
-
trong khi tôi
-
sum1:=sum1 + nums1 [i]
-
i:=i + 1
-
-
trong khi j
-
sum2:=sum2 + nums2 [j]
-
j:=j + 1
-
-
return (res + tối đa của sum1, sum2) mod 10 ^ 9 + 7
Ví dụ
Hãy cùng chúng tôi xem cách triển khai sau đây để hiểu rõ hơn
def solve(nums1, nums2):
M, N = len(nums1), len(nums2)
sum1, sum2 = 0, 0
i, j = 0, 0
res = 0
while i < M and j < N:
if nums1[i] < nums2[j]:
sum1 += nums1[i]
i += 1
elif nums1[i] > nums2[j]:
sum2 += nums2[j]
j += 1
else:
res += max(sum1, sum2) + nums1[i]
i += 1
j += 1
sum1 = 0
sum2 = 0
while i < M:
sum1 += nums1[i]
i += 1
while j < N:
sum2 += nums2[j]
j += 1
return (res + max(sum1, sum2)) % 1000000007
nums1 = [3,5,6,9,11]
nums2 = [5,7,9,10]
print(solve(nums1, nums2)) Đầu vào
[3,5,6,9,11], [5,7,9,10]
Đầu ra
35
