Giả sử chúng ta có một tập hợp các điểm Descartes trong một danh sách được gọi là các điểm. Chúng ta phải sắp xếp chúng dựa trên các góc phân cực của chúng. Các góc cực thay đổi trong phạm vi 0 và 2 * PI. Nếu một số điểm có cùng góc cực, thì hãy sắp xếp chúng dựa trên khoảng cách của điểm đó so với điểm gốc.
Vì vậy, nếu đầu vào giống như điểm =[(1,1), (1, -2), (- 2,2), (5,4), (4,5), (2,3), (- 3,4)],
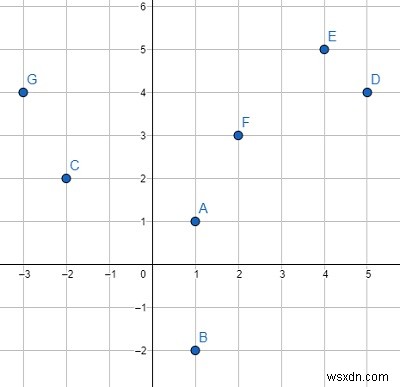
thì đầu ra sẽ là [(5, 4), (1, 1), (4, 5), (2, 3), (-3, 4), (-2, 2), (1, -2) ]
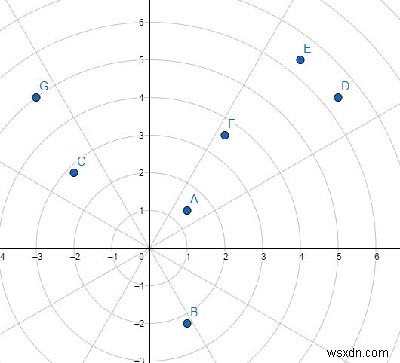
Để giải quyết vấn đề này, chúng tôi sẽ làm theo các bước sau -
- Xác định một phím chức năng so sánh (). Điều này sẽ mất x
- atan:=tan-nghịch đảo của x [1] / x [0]
- trả về cặp (atan, x [1] ^ 2 + x [0] ^ 2) nếu atan> =0 ngược lại (2 * pi + atan, x [0] ^ 2 + x [1] ^ 2)
- sau đó sắp xếp các điểm bằng phím chức năng so sánh ()
Ví dụ
Hãy cùng chúng tôi xem cách triển khai sau để hiểu rõ hơn -
nhập mathdef giải (điểm):def key (x):atan =math.atan2 (x [1], x [0]) return (atan, x [1] ** 2 + x [0] ** 2) if atan> =0 else (2 * math.pi + atan, x [0] ** 2 + x [1] ** 2) trả về được sắp xếp (điểm, khóa =khóa) điểm =[(1,1) , (1, -2), (- 2,2), (5,4), (4,5), (2,3), (- 3,4)] print (giải (điểm))Đầu vào
[(1,1), (1, -2), (- 2,2), (5,4), (4,5), (2,3), (- 3,4)]Đầu ra
[(5, 4), (1, 1), (4, 5), (2, 3), (-3, 4), (-2, 2), (1, -2)]
