Giả sử chúng ta có các điểm bên ngoài của một đa giác theo thứ tự theo chiều kim đồng hồ. Chúng ta phải kiểm tra những điểm này có tạo thành một đa giác lồi hay không. Một đa giác được cho là lõm nếu bất kỳ góc nào bên trong của nó lớn hơn 180 °.
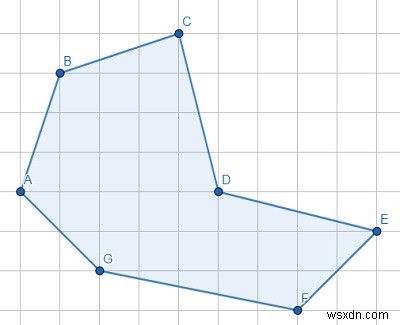
Từ sơ đồ này, rõ ràng là đối với mỗi ba điểm liên tiếp, góc bên trong không quá 180 ° ngoại trừ CDE.
Vì vậy, nếu đầu vào giống như điểm =[(3,4), (4,7), (7,8), (8,4), (12,3), (10,1), (5,2 )], thì đầu ra sẽ là True.
Để giải quyết vấn đề này, chúng tôi sẽ làm theo các bước sau -
- n:=kích thước của điểm
- đối với tôi trong phạm vi từ 0 đến kích thước của điểm, hãy thực hiện
- p1:=điểm [i-2] khi tôi> 1, ngược lại điểm [n-2]
- p2:=điểm [i-2] khi tôi> 0, nếu không thì điểm [n-1]
- p3:=điểm [i]
- nếu góc giữa các điểm (p1, p2, p3)> 180, thì
- trả về True
- trả về Sai
Ví dụ
Hãy cùng chúng tôi xem cách triển khai sau để hiểu rõ hơn -
import math def get_angle(a, b, c): angle = math.degrees(math.atan2(c[1]-b[1], c[0]-b[0]) - math.atan2(a[1]-b[1], a[0]-b[0])) return angle + 360 if angle < 0 else angle def solve(points): n = len(points) for i in range(len(points)): p1 = points[i-2] p2 = points[i-1] p3 = points[i] if get_angle(p1, p2, p3) > 180: return True return False points = [(3,4), (4,7),(7,8),(8,4),(12,3),(10,1),(5,2)] print(solve(points))
Đầu vào
[(3,4), (4,7),(7,8),(8,4),(12,3),(10,1),(5,2)]
Đầu ra
True
